Na figura ao lado temos um sistema com três componentes funcionando independemente, com confiabilidades Obtenha a confiabilidade do sistema.
Passo 1
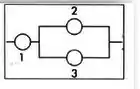
Vamos olhar para a figura e interpretar:
Os componentes 2 e 3 estão em paralelo e o componente 1 está em série com o “box” 23. Certo?
Já deu pra notar então que vamos ter que dividir esse problema em dois:
1º Encontrar a confiabilidade do sistema 23 (paralelo).
2º Encontrar a confiabilidade do sistema 1 e “box”
Note que esse para esse “box” utilizaremos a confiabilidade que calcularmos de 2 e 3.
Vamos então?
Passo 2
Confiabilidade Sistema 2-3:
Como está em paralelo, sabemos que:
Passo 3
Confiabilidade Sistema 1 – “box”
Como está em série, sabemos que:
Resposta
Exercícios de Livros Relacionados
Eixos são classificados em termos de ferramenta de usinagem que foi usada para fabricar o eixo e obedecer aos requisitos de acabamento de superfície e de bordas arredondadas.Se A ,BeC forem eventos mu
Está sendo testado um novo processo de detectar mais acuradamente a respiração anaeróbica em células. O novo processo é importante devido à sua alta acurácia, à sua falta de experimentação extensiva e
Amostras de vidrarias de laboratório são embaladas em pacotes pequenos e leves ou em pacotes grandes e pesados. Suponha que 2 e 1% da amostra despachada em pequenos e grandes pacotes, respectivamente,
Eixos são classificados em termos de ferramenta de usinagem que foi usada para fabricar o eixo e obedecer aos requisitos de acabamento de superfície e de bordas arredondadas.Se A ,BeC forem eventos mu
Um lote contém 15 moldes provenientes de um fornecedor local e 25 moldes provenientes de um fornecedor de um estado vizinho. Dois moldes são selecionados ao acaso, sem reposição, do lote de 40. Seja A