Exercícios Resolvidos de Teoria da Confiabilidade

Enunciado

Suponha um sistema composto por 4 elementos. O elemento 1 e o elemento 4 são indispensáveis para o fucionamento do sistema. O elemento 2 pode falhar sem impedir o funcionamento do sistema, idem para o elemento 3. Mas os elementos 2 e 3 não podem parar de funcionar ao mesmo tempo. Qual a confiabilidade do sistema? Assuma todas as confiabilidades como .

Passo 1

Vamos pensar no que foi falado. Elemento 1 e 4 são indispensáveis para o funcionamento, ou seja, são as estruturas sem paralelos. Já os elementos 2 e 3 podem falhar separadamente mas nunca ao mesmo tempo, então são elementos em paralelo. Desenhando temos algo assim:

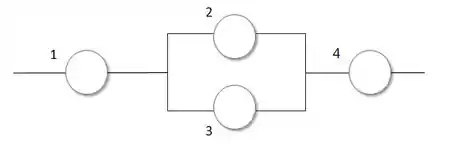
Passo 2

Vamos calcular primeiro a confiabilidade do Box em paralelo, ou seja, elementos 2 e 3:

Passo 3

Agora podemos colocar o elemento 1, o resultante do Box e o elemento 4 em série e teremos:

Resposta

Exercícios de Livros Relacionados

Eixos são classificados em termos de ferramenta de usinagem que foi usada para fabricar o eixo e obedecer aos requisitos de acabamento de superfície e de bordas arredondadas.Se A ,BeC forem eventos mu

Está sendo testado um novo processo de detectar mais acuradamente a respiração anaeróbica em células. O novo processo é importante devido à sua alta acurácia, à sua falta de experimentação extensiva e

Amostras de vidrarias de laboratório são embaladas em pacotes pequenos e leves ou em pacotes grandes e pesados. Suponha que 2 e 1% da amostra despachada em pequenos e grandes pacotes, respectivamente,

Um lote contém 15 moldes provenientes de um fornecedor local e 25 moldes provenientes de um fornecedor de um estado vizinho. Dois moldes são selecionados ao acaso, sem reposição, do lote de 40. Seja A