Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Sonntag, R.E. e Borgnakke, C. -Fundamentos da Termodinâmica- Ed: 1º - Capítulo 9.Problemas - Ex. 18

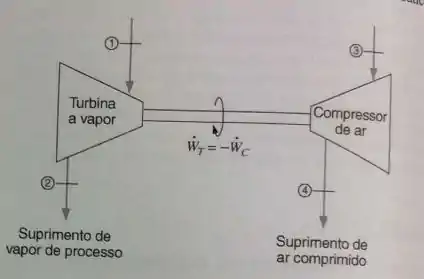
Um determinado processo industrial requer um suprimento permanente de vapor d’água saturado a 200   k P a , a uma taxa de 0,5   k g / s . Também é requerido um suprimento permanente de ar comprimido a 500   k P a , a uma taxa de 0,1   k g / s . Ambos devem ser disponibilizados pelo conjunto turbina/compressor mostrado na Fig. P9.18. Vapor d´água é expandido na turbina para fornecer a potência necessária para acionar o compressor de ar, e o vapor exausto deixa a turbina no estado desejado. O ar entra no compressor na condição ambiente, 100   k P a e 20 ° C . Determine a temperatura e a pressão do vapor requeridas na entrada da turbina, considerando que tanto a turbina quanto o compressor são reversíveis e adiabáticos.

Passo 1

Fala pessoal, tudo certinho? vamos responder mais uma questão, então prepara o material e vamos responder!!

São fornecidos os seguintes dados para adiabático expandido a vapor em uma turbina para alimentar o compressor de ar adiabático:

m 2 ' = 0,5 k g s

P 2 = 200   k P a

P 3 = 100   k P a

T 3 = 293   K

P 4 = 500   k P a

m 4 ' = 0,1 k g s

Da tabela de propriedades A.5. podemos encontrar o calor específico do ar e o expoente adiabático:

C p = 1,004 k J k g   K

Com isso, o k é igual a 1,4 . Calculando a temperatura de saída do compressor de ar:

T 4 = T 3 ∙ P 4 P 3 k - 1 k = 293 ∙ 500 100 1,4 - 1 1,4

Portanto, nós temos que

T 4 = 464   K

Calculando a taxa de trabalho do compressor de ar:

W ' = m 4 ' ∙ C p ∙ T 3 - T 4 = 0,1 ∙ 1,004 ∙ 293 - 464

Com isso, nós temos o seguinte resultado

W ' = - 17,17   k W

Passo 2

Da tabela de água superaquecida B.1.3. correspondente a P 2 = 200   k P a , podemos encontrar a entropia e a entalpia específicas do vapor saturado do estágio 2:

h 2 = 2706,63 k J k g

s 2 = 7,1271 k J k g   K

Podemos calcular a entalpia específica do estágio 1 da equação de energia:

h 1 = h 2 - W ' m 2 ' = 2706,63 + 17,17 0,5 = 2741 k J k g

Como temos P 2 = 200   k P a e h 2 = 2706,63 k J k g , nós podemos encontrar a temperatura para esse estágio

T = 120,23 ° C

Para o caso de P 2 = 200   k P a e h = 2768,80 k J k g ,

T = 150 ° C

Calculando a temperatura de entrada usando o método de interpolação linear:

T 1 = 120,23 + 2741 - 2706,63 2768,80 - 2706,63 ∙ 150 - 120,23 = 137 ° C

E calculando a pressão de entrada usando o método de interpolação linear:

P 1 = 300 + 2741 - 2706,63 2768,80 - 2706,63 ∙ 300 - 200 = 255   k P a

Resposta

T 1 = 137 ° C

P 1 = 255   k P a

Exercícios de Livros Relacionados

Uma turbina com potência de 150k W opera de modo adiabático e reversível. A turbina é alimentada com vapor d’água a 700 ° C e 2M P a e a exaustão da turbina é encaminhada para um trocador de calor que
A Fig. P9.42 mostra o esquema de um ciclo motor a vapor d’água que opera a pressão supercrítica. Em primeira aproximação, pode-se admitir que os processos que ocorrem na turbina e na bomba são adiabát
A Fig. P9.39 exemplifica uma técnica utilizada na operação, em cargas parciais, de turbinas a vapor. Ela consiste em estrangular o vapor d’água de alimentação até uma pressão inferior à da linha. Admi
89- Uma bomba de calor deve ser utilizada para aquecer uma residência no inverno e depois, funcionando em operação reversa, para resfriar a residência no verão.A temperatura interna deve ser mantida a
91- Um tanque com volume de 10m 3 contém, inicialmente, ar a 500k P a e 600K e funciona como fonte quente para um ciclo de Carnot que rejeita calor a 300K .A temperatura alta do ciclo de Carnot é semp