Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 4.Problemas - Ex. 155

Dois tanques adiabáticos de 10 p é s 3 estão conectados por uma válvula. Inicialmente, um tanque contém água a 450 psia com título de 10%, enquanto o segundo contém água a 15 psia com título de 75%. A válvula é então aberta, permitindo que o vapor de água do tanque de alta pressão mova-se para o tanque de baixa pressão até que a pressão nos dois tanques seja igual. Determine a pressão final e a massa final em cada tanque.

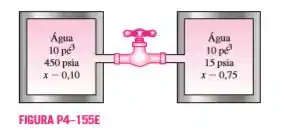
Passo 1

Inicialmente, vamos encontrar algumas propriedades relacionadas a água para os dois tanques nas tabelas de vapor, note que temos uma mistura líquido-vapor em cada tanque, assim, teremos:

  • Tanque A – 450 psia:

    • u 1 , A = u l + x u l v = 435,67   B t u / l b m + 0,10 × 683,52   B t u / l b m = 504,02   B t u / l b m

    υ 1 , A = υ l + x υ l v = 0,01955   p é s 3 / l b m × 0,10 × 1,0324 - 0,01955 p é s 3 / l b m = 0,1208   p é s 3 / l b m

  • Tanque B – 15 psia:

u 2 , B = u l + x u l v = 181,16   B t u / l b m + 0,75 × 896,52   B t u / l b m = 853,55   B t u / l b m

υ 2 , B = υ l + x υ l v = 0,0 1672   p é s 3 / l b m × 0 , 75 × 26,297 - 0,01672 p é s 3 / l b m = 19,727   p é s 3 / l b m

Com isso, saberemos a massa encontrada dentro dos tanques que será dada por:

m = m 1 , A + m 1 , B = V A υ 1 , A + V B υ 1 , B = 10   p é s 3 0,1208   p é s 3 / l b m + 10 p é s 3 19,727   p é s 3 / l b m = 83,3   l b m

Passo 2

Temos que o balanço de energia para um sistema fechado pode ser dado como:

Δ U + E C + E P s i s t e m a = Q + W  

Adotando os tanques como sistema podemos desprezar a variação de energia cinética e potencial, além de que não há trocas de calor com as vizinhanças e não tem trabalho sendo realizado, assim:

Δ U ^ = 0

U 1 = U 2

Pelas condições iniciais, conseguimos descobrir que:

U 1 = m 1 , A u 1 , A + m 1 , B u 2 , B = 82,79   l b m × 504,02   B t u / l b m + 0,51   l b m × 853,55   B t u / l b m = 42155   B t u

Como temos que as energias internas no início e no final serão iguais, vamos descobrir a energia interna e volume específico, daí:

u 1 = u 2 = U 1 m = 42155   B t u 83,3   l b m = 506,06   B t u / l b m

υ 1 = υ 2 = V m = 20   p é s 3 83,3   l b m = 0,24   p é s 3 / l b m

Passo 3

Buscando por essa energia interna e esse volume específico nas tabelas de vapor, vamos encontrar uma pressão final de P 2 = 313   p s i a .

A massa de cada tanque no final será a massa dividia por 2, pois ela será dividida igualmente entre os tanques após a mistura, daí:

m 2 , A = m 2 , B = m 2 = 41,65   l b m

Resposta

A pressão final será de 313 psia e a massa final em cada tanque é de 41,65 lbm.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

128- Um tanque rígido e selado contém amônia a 0° C e com título igual a 50% . O tanque é, então, aquecido até a temperatura atingir 100° C . Determine o estado final da amônia, o trabalho realizado e
Considere uma amostra de gás Hélio. Inicialmente, o volume da amostra, a temperatura e a pressão no Hélio são iguais a 0,025m 3 , 350K e 125k P a . O gás expande politropicamente n = 1,667 até que a p
Um conjunto cilindro-pistão contém oxigênio. Inicialmente, o volume interno do conjunto é 0,1m 3 e o ar apresenta temperatura e pressão iguais a 100 ° C e 300 k P a . O oxigênio é então comprimido, nu
Um conjunto cilindro – pistão contém água. Inicialmente, o volume interno do conjunto é 0,025m 3 e a água se encontra como vapor saturado a 180 ° C . O vapor expande num processo politrópico, com n =
Um conjunto cilindro-pistão contém ar. Inicialmente, o volume, a pressão e a temperatura do ar são iguais a 0,001m 3 , 100k P a e 300 K . O ar é então comprimido, num processo onde p v 1,25 = C , até