Um gás ideal em um dado estado se expande até um determinado volume final, depois a uma temperatura constante. Em qual caso o trabalho é maior?

Devemos lembrar que o trabalho de fronteira é obtido pela soma de todos os trabalhos diferenciais do estado inicial ao final de um processo:

Lembre-se que o significado de uma integral é a área abaixo de uma curva. Logo, o trabalho de fronteira pode ser entendido como a área a abaixo da curva de um diagrama Pressão-Volume.

Vamos, então, analisar os dois casos citados no enunciado.

Primeiramente, temos uma expansão (aumento de volume) a uma pressão constante P1:

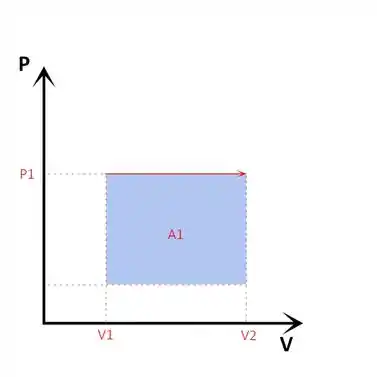
Posteriormente, temos uma expansão a uma temperatura constante, com a pressão variando de P1 a P2. Note temos os mesmos volumes inicial e final do caso anterior:

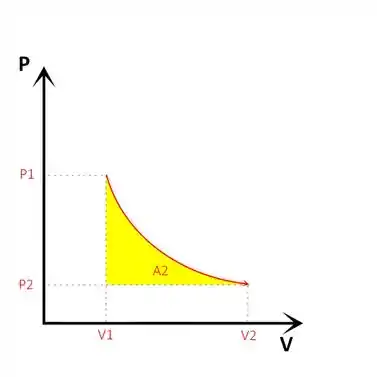
Como foi dito anteriormente, o trabalho de fronteira pode ser entendido como a área embaixo das curvas dos dois processos.

É possível notar que, claramente, a área abaixo da curva da expansão a pressão constante é maior do que a área abaixo da curva a temperatura constante.