Enunciado
Termodinâmica - Çengel - Termodinâmica - Ed: 7º - Capítulo 9.Problemas - Ex. 103
Uma usina de potência com turbina a gás operando em um ciclo Brayton simples tem uma razão de pressão igual a . Em um certo momento, ar entra no compressor a. A temperatura máxima do ciclo é de , o compressor tem uma eficiência isentrópica de e a turbina tem uma eficiência isentrópica igual a . Considere as propriedades constantes para o ar a , com , , , .
(a) Represente graficamente o diagrama para o ciclo.
(b) Considerando que a produção de potência líquida corresponde a , determine a vazão volumétrica do ar dentro do compressor, em .
(c) Considerando um compressor com velocidade de entrada e área de fluxo estabelecidas, explique o efeito do aumento da temperatura de entrada do compressor (ou seja, durante o funcionamento no verão versus funcionamento no inverno) sobre a vazão mássica de entrada e da potência útil. Todos os outros parâmetros do problema são os mesmos.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Bom... Para esboçar o nosso ciclo em um diagrama , temos que saber primeiramente se os processos de compressão e expansão serão totalmente isentrópicos ou não.
Como no enunciado já nos foram dadas as eficiências isentrópicas tanto da turbina quanto do compressor, sabemos que teremos o estado representando o real e o ideal para a saída do compressor e o estado representando o real e o ideal na saída da turbina.
O exercício nos disse que o ciclo opera com e que a pressão na entrada do compressor é de . Sabemos que a baixa pressão ocorre no processo e a pressão maior no processo . Portanto:
E como:
Temos que:
Como o ar entra no compressor a , temos que:
Sabemos também que:
A temperatura máxima do ciclo é de. A maior temperatura em um ciclo Brayton ocorre na entrada da turbina (estado ), portanto:
Sabendo estes dados, temos que seu diagrama é dado por:
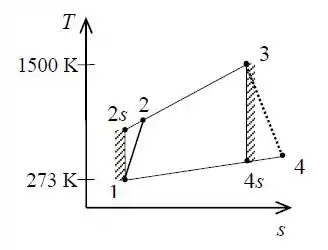
Passo 2
Agora vamos analisar os processos:
O processo é uma compressão isentrópica, logo:
Temos que:
Logo:
Substituindo os valores temos que:
Passo 3
Achamos a temperatura ideal, porem o processo não é ideal, logo:
Substituindo os valores, temos que:
A temperatura real na saída do compressor será:
Passo 4
Podemos calcular a pressão do estado a partir da relação do processo isentrópico. Para a expansão , temos que:
Como:
Substituindo os valores, temos que:
Passo 5
Achamos a temperatura ideal, porem o processo não é ideal, logo:
Substituindo os valores, temos que:
A temperatura real na saída da turbina será:
Passo 6
Sabendo que a potência é dada por:
Temos que:
O volume específico será:
Sabendo que a vazão pode ser dada pelo produto entre o fluxo de ar pelo volume especifico, temos que:
Passo 7
Para descobrir o efeito do aumento de temperatura na entrada do compressor, vamos fazer algumas considerações.
Da equação do gás ideal, temos que:
Portanto, é possível notar que a temperatura é inversamente proporcional à densidade do gás.
O fluxo de massa pode ser dado por:
Como a velocidade e a área são constantes, podemos dizer que a densidade é diretamente proporcional ao fluxo.
Logo:
O fluxo será inversamente proporcional à temperatura. Ou seja, o aumento de temperatura na entrada do compressor provoca uma diminuição no fluxo de ar.
A potência é dada por:
Portanto, podemos dizer que a potência é diretamente proporcional ao fluxo de ar. Sendo assim, temos que:
Logo:
O aumento da temperatura diminui o fluxo de ar na entrada do compressor diminuindo assim a potência líquida.
Resposta
O aumento da temperatura diminui o fluxo de ar na entrada do compressor diminuindo assim a potência líquida.