Equilíbrio multifásico e multicomponente
Produzido por Rafael Cardoso BrandãoTeoria
Diagrama para mais de uma fase e mais de um componente
Vamos ver como fica o equilíbrio de um sistema com mais de um componente e mais de uma fase. Para podermos ter uma ideia de tal sistema vamos pegar uma faixa de temperatura e pressão onde dois componentes (1 e 2) apresentam tanto a fase vapor quanto líquido e colocaremos essas informações no diagrama abaixo.
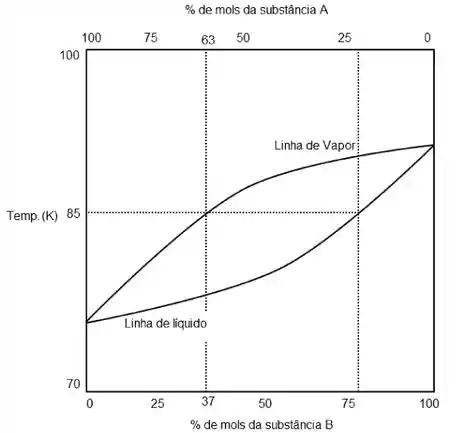
Esse diagrama pode ser um pouco difícil de entender então vamos num passo-a-passo. Primeiro temos que esse diagrama é dado para uma pressão constante. Segundo, a temperatura varia na vertical enquanto a concentração da substância aumenta da direita para a esquerda (o inverso ocorre com porque a soma de ambos deve ser igual a 100%).
Também é crucial entender as linhas de vapor (acima) e líquido (abaixo). Essas linhas representam o quanto de vapor e líquido existem em cada fase da nossa mistura, como assim?

Observe que a temperatura de 85K foi marcada. À temperatura de 85K qual será a concentração da substância na fase vapor? Para responder basta traçar uma horizontal a partir de 85K até interceptar a linha vapor (mais elevada) e depois uma vertical até a base do nosso diagrama. Ao fazer isso vemos que a concentração da substância na fase vapor é de 37% e, consequentemente, a concentração de na fase vapor é de 63% pois a soma deve dar 100%.
E para a fase líquida? Você consegue ter uma ideia de qual seria a concentração de cada componente a 85K?
Para a substância a concentração na fase líquida nessa temperatura e pressão seria de mais ou menos 24% enquanto para a substância 76%.
Equilíbrio multifásico e multicomponente
Para definir o equilíbrio de um sistema como o apresentado acima vamos utilizar novamente a função de Gibbs, mas agora um novo termo será adicionado a ela, o potencial químico (). Portanto, a função de Gibbs para os componentes e e fases 1 e 2 fica da forma:
A variação total da função de Gibbs é igual a zero pois estamos no equilíbrio.
e
Como estamos trabalhando no equilíbrio podemos considerar a temperatura, pressão e número de mols do componente constantes, então suas derivadas vão ser iguais a zero, assim, vamos ter que.
Assim, a exigência para o equilíbrio é que o potencial químico de cada fase deve ser igual. Isso vale para todos os componentes e fases, assim o resultado é.
Podemos também achar o equilíbrio pela fugacidade, igualando a fugacidade molar parcial da substância nas suas duas fases.
Aqui é importante ressaltar que a fugacidade molar parcial de uma substância () é igual a concentração molar () vezes a fugacidade da substância pura (.
Essa equação é conhecida como Lei de Lewis-Randall.
Regra das fases de Gibbs
Se lembra que um estado termodinâmico é especificado quando temos duas propriedades intensivas independentes?
Esse caso valia para o caso de soluções que não havia mistura. Então como vamos saber quantas propriedades devemos ter para o caso de uma mistura?
A regra das fases de Gibbs nos permite descobrir exatamente isso, quantas propriedades intensivas precisam ser especificadas para determinar um estado termodinâmico. E funciona de uma forma bem simples a partir de uma equação bem simples e 3 parâmetros.
- – Número de fases
- – Variância
- – Número de componentes
A regra funciona assim, para uma substância pura temos que , se tivermos uma fase, líquida por exemplo, vamos ter . Sendo assim, podemos ver que , ou seja, são necessárias duas propriedades intensivas para definirmos o estado, que nem já vimos antes!
Agora vamos pegar um exemplo com dois componentes e três fases então , nesse caso precisamos apenas de uma propriedade intensiva fixada para termos um estado definido.
Equilíbrio multifásico e multicomponente
Regra das fases de Gibbs
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração própria
Um sistema é composto por 3 componentes nas fases líquida e vapor, quantas propriedades intensivas são necessárias para estabelecer um estado termodinâmico?
Passo 1
Essa é uma questão clássica da regra de Gibbs que é dada por
- – Número de fases (duas).
- – Variância (o que queremos).
- – Número de componentes (três).
Ou seja, são necessárias três propriedades intensivas para que o estado termodinâmico seja definido.
Resposta
São necessárias três propriedades intensivas para que o estado termodinâmico seja definido.
Exercício Resolvido #2
Elaboração própria
Uma substância pura está no seu ponto triplo (equilíbrio entre vapor, líquido e sólido) quantas propriedades intensivas são necessárias para definir esse ponto triplo?
Passo 1
Aqui está mais uma questão sobre a regra de Gibbs. Vamos ter
- – Número de fases (três).
- – Variância (o que queremos).
- – Número de componentes (um).
Ou seja, no ponto triplo o estado termodinâmico da substância pura já está definido!! Mas observe que existem vários estados sólidos para uma mesma substância por isso existem diversos pontos triplos. Por isso o exercício coloca em evidência que esse ponto triplo trata de líquido, sólido e vapor, assim, existe apenas um estado.
Resposta
Nenhuma, no ponto triplo o estado termodinâmico já está definido.
Exercício Resolvido #3
Elaboração própria
Num sistema com múltiplos componentes e múltiplas fases o que aconteceria caso o potencial químico de algum desses componentes fosse diferente nas suas fases?
Passo 1
Como visto na teoria quando estamos no equilíbrio temos que . E a função de Gibbs é dada por:
No caso de mesma pressão e temperatura vamos ter
Ou seja, o equilíbrio irá depender apenas dos potenciais químicos.
Passo 2
A variação total da função de Gibbs é igual a zero pois estamos no equilíbrio. Será a soma duas fases (1 e 2).
e
Como
e
Temos
Porém se o potencial químico de uma fase de um componente for diferente do potencial da outra fase, o sistema não estará mais em equilíbrio forçando uma passagem de massa de uma fase para a outra.
Resposta
O sistema não estará mais em equilíbrio forçando uma passagem de massa de uma fase para a outra.
Exercício Resolvido #4
Elaboração própria
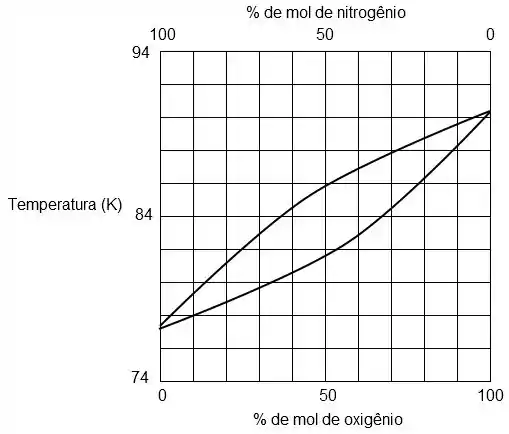
Observe atentamente o diagrama abaixo representando o equilíbrio de nitrogênio e oxigênio à pressão de 0,1MPa e responda qual a temperatura de vaporização para o caso de 100% oxigênio e para o caso 100% nitrogênio.
Passo 1
Primeiro vamos olhar o caso em que temos 100% de oxigênio. Nesse caso estamos no extremo direito do diagrama.
Vamos lembrar que a linha superior é a linha vapor e a linha inferior a linha líquida, perceba que quando temos um componente puro as duas linhas se encontram e o ponto de encontro é o próprio ponto de vaporização.
Portanto, para o caso de 100% oxigênio a vaporização ocorre a mais ou menos 90,2 K.
Já para o casa de 100% de nitrogênio estamos trabalhando no extremo esquerdo do diagrama, com isso o ponto de vaporização (que é o encontro das curvas – no caso de substância pura) será na temperatura de mais ou menos 77,3 K.
Resposta
Para o caso de 100% oxigênio a vaporização ocorre a mais ou menos 90,2 K.
Já para o casa de 100% de nitrogênio o ponto de vaporização será na temperatura de mais ou menos 77,3 K.
Exercício Resolvido #5
Elaboração própria
Abaixo está representado o diagrama de equilíbrio do oxigênio e nitrogênio para as fases líquida e vapor a pressão 0,1MPa.
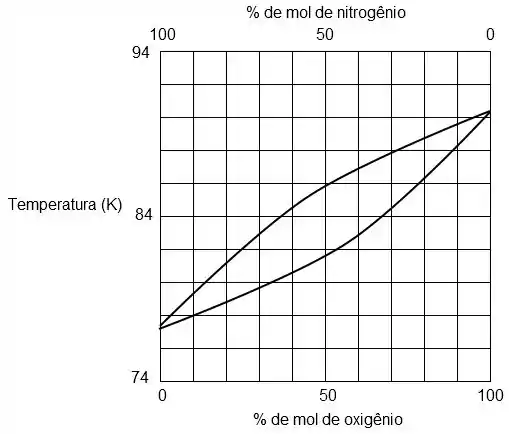
A partir da leitura do diagrama e supondo que a mistura tem 20% de nitrogênio e 80% de oxigênio, determine a composição das duas fases nas temperaturas de 79K e 81K.
Passo 1
A coisa mais importante nesse tipo de exercício é saber identificar corretamente os pontos que estamos trabalhando, assim, o resto fica mamatinha..
Então vamos lá, vamos procurar a reta vertical que representa a mistura 20% nitrogênio e 80% oxigênio. Lembrando que a linha superior é a de vapor e a inferior a de líquido.
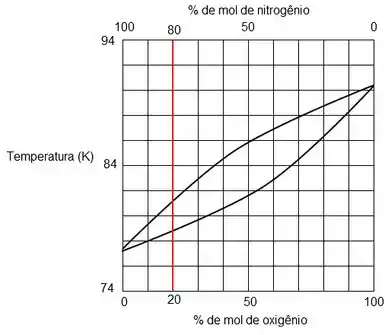
Beleza, achamos a reta que contém a composição da mistura.
Passo 2
Agora vamos traçar a reta horizontal que representa a temperatura de 79K.
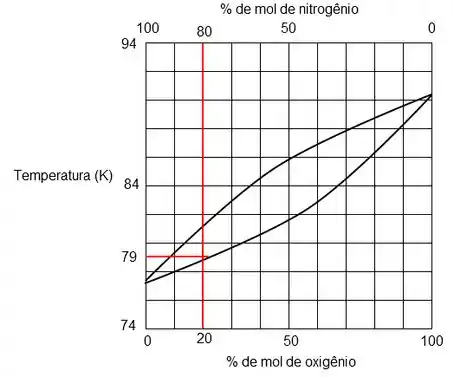
Perceba que a interseção das retas acontece entre as linhas vapor e líquido logo existirá uma mistura das fases, caso a interseção fosse acima da linha vapor então teremos somente vapor e abaixo da linha líquido teremos apenas líquidos. Nós vamos achar a proporção no vapor fase achando a interseção da linha de vapor com a reta da temperatura horizontal, e do líquido se faz com a interseção da linha líquido. Vamos fazer isso na próxima etapa.
Passo 3
Achamos dois pontos de interseção, um referente à fase vapor e outra à fase líquida.
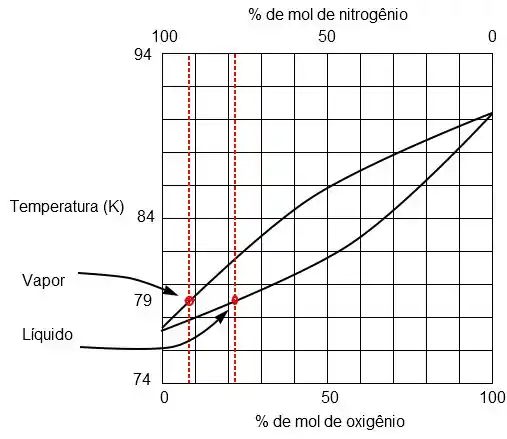
Então a composição da fase vapor será de mais ou menos 9% de oxigênio e 91% de nitrogênio, já a fase líquida terá a composição de 11% de oxigênio e 89% de nitrogênio.
Passo 4
Agora vamos fazer a mesma coisa para a temperatura de 81K. Dessa vez vamos achar direto o ponto de interseção.
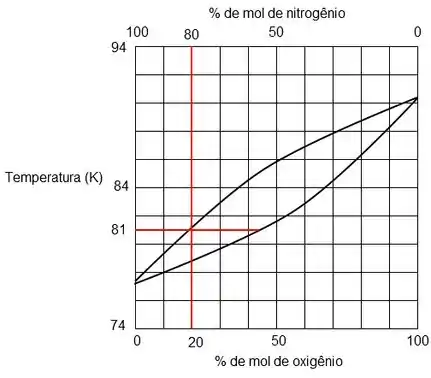
Passo 5
Agora vamos achar os dois pontos de interseção correspondentes à cada fase.
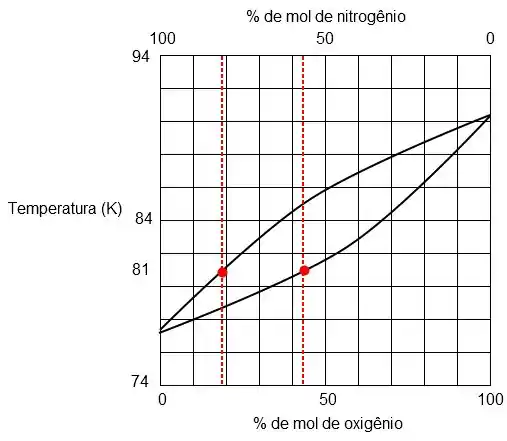
Logo a composição da fase vapor para a temperatura de 81K é de 19% de oxigênio e 81% de nitrogênio. Já para a fase líquida será de 43% de oxigênio e 57% de nitrogênio.
Resposta
A composição da fase vapor a 79K será de mais ou menos 9% de oxigênio e 91% de nitrogênio, já a fase líquida terá a composição de 11% de oxigênio e 89% de nitrogênio.
Logo a composição da fase vapor para a temperatura de 81K é de 19% de oxigênio e 81% de nitrogênio. Já para a fase líquida será de 43% de oxigênio e 57% de nitrogênio.
Exercício Resolvido #6
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.451 – Exemplo 13.3.
Ar (suposto como 21% de e 79% de ) é resfriado até 80K a pressão de 0,1 MPa. Calcular a composição da fase líquida e vapor nesta condição. Admita o modelo de Raoult-gás perfeito. Dados: ; .
Passo 1
Lembrando a Regra de Raoult temos que:
Além disso temos também que a fase líquida é composta por
E a fase vapor
Assim temos o nosso modelo para resolver a questão.
Passo 2
Substituir os valores de pressão e pressão de saturação
Passo 3
Utilizar as duas outras equações para achar os valores
Substituindo os valores temos que
Multiplicando a segundo equação por 0,73 e subtraindo da primeira temos
Logo
Passo 4
Agora é só voltar na relação entre a fase líquida e vapor para achar a concentração da fase líquida
Perceba que a soma da 100%, que é quanto tem que dar mesmo!
Resposta
Exercício Resolvido #7
Elaboração própria
Um sistema é composto por pelos refrigerantes e , a pressão desse sistema é igual a 50 kPa (0,05 MPa) e as pressões de saturação nesse estado de equilíbrio são de 0,039 MPa e 0,064 MPa, respectivamente. Sabendo que ambos coexistem com seus estados de vapor e líquido, determine a composição do líquido e do vapor.
Passo 1
O problema pede a composição de ambas as fases, líquida e vapor, portanto, podemos escrever:
e da atmosfera, fase vapor
Como a pressão de saturação e a pressão atmosférica também foram dadas então iremos utilizar a regra de Raoult
Passo 2
Agora vamos substituir na equação e ver o que achamos, para o
Para o
Passo 3
Agora temos mais duas equações e com as duas equações das fases vapor e líquido temos 4 equações com 4 incógnitas:
Vamos substituir as duas últimas na primeira obtendo:
Multiplicando a segunda por 0,78 e subtraindo da primeira
Logo
Como a soma deve dar 1
Consequentemente para a fase líquida do
e para o
Resposta
Exercício Resolvido #8
Gordon Van Wylen, Richard Sonntag e Claus Borgnakke, Fundamentos da termodinâmica clássica, Tradução da 4ª ed. americana. São Paulo: Edgard Blucher, 1995, pp.449 – Exemplo 13.2. (Adaptada)
Calcule as composições das fases (líquido-vapor) na mistura metano-monóxido de carbono a 100°C e 4MPa sabendo que o monóxido de carbono puro é um gás e que o metano puro é um líquido nesse estado. Admita o modelo de solução ideal nas duas fases. Dados:
- ; .
- ; .
- (monóxido de carbono como líquido hipotético)
- (metano como vapor hipotético)
Passo 1
Aqui é crucial perceber que nessa temperatura e pressão o monóxido de carbono é vapor enquanto o metano é líquido, por isso o problema forneceu uma fugacidade hipotética, pois eventualmente vamos utilizar a equação
Mesmo que não exista fase líquida ou vapor, existe uma fugacidade hipotética associada áquela situação.
Passo 2
Vamos achar as temperaturas relativas e pressões reduzidas para cada componente.
Passo 3
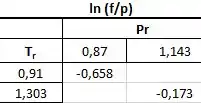
Utilizando a tabela fornecida no problema podemos calcular a fugacidade de cada componente (associadas às suas fases que realmente existem).
Para o metano:
Para o monóxido de carbono:
Passo 4
Utilizar as fugacidades calculadas e fornecidas para achar uma relação entre as composições das fases
Para o metano
Para o monóxido de carbono
Passo 5
Utilizar as relações
Para achar as composições das fases
Substituindo na primeira equação
Multiplicando a segunda por 0,4667 teremos
Subtraindo as duas
Portanto
E