Na viga Gerber abaixo, determine o diagrama de Esforços cortantes.
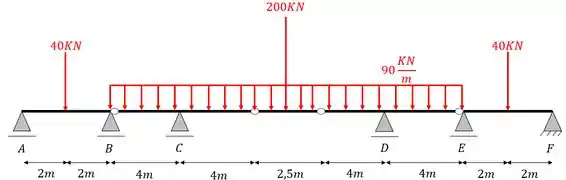
Passo 1
Como podemos ver, resolvemos essa viga no exercício anterior, mas com o intuído de terminar todas as suas reações de apoio. Agora o nosso intuito é prosseguir exatamente a partir do final do exercício anterior, ou seja, após ter calculado todas as reações de apoio, como determinamos os esforços cortantes existentes na viga?
Lembrando o nosso passo a passo, veremos que esse se trata do último passo dado, como indicamos abaixo
- Primeiro quebramos as nossas rótulas e definimos apoios fictícios que sejam coerentes, ou seja, que tornem todas as vigas isostáticas e que também tenham um local para transferir a sua carga, já que se trata de um apoio fictício, ou seja, ele irá transferir a sua carga para algum lugar.
- Depois que tivermos todas as vigas isostáticas e com apoios fictícios, transferimos os seus carregamentos para as vigas respectivas e definimos uma ordem de solução para a nossa viga, começando sempre da viga mais externa e indo até a viga mais interna.
- Por fim, veja só, temos todas as vigas isostáticas, seus apoios fictícios, suas transferências e uma ordem de solução, agora é só começarmos a calcular as reações de apoio seguindo corretamente a ordem de solução definida.
- Diagrama de esforços cortante e de Momentos fletores
vamos agora partir para a solução do nosso problema.
Passo 2
Já temos a divisão das nossas vigas em vigas mais simples, assim como também sabemos que a nossa viga é simétrica tanto em carregamento quanto em formato, o que sabemos que indica que não precisamos resolver a nossa viga Gerber toda, mas apenas metade e depois faremos simetria para resolver o resto. Já calculamos todas as reações de apoios normais e fictícias, o que significa que temos a seguinte situação no final do exercício anterior
- Viga 1 = Viga 5
- Viga 2 = Viga 4
- Viga 3
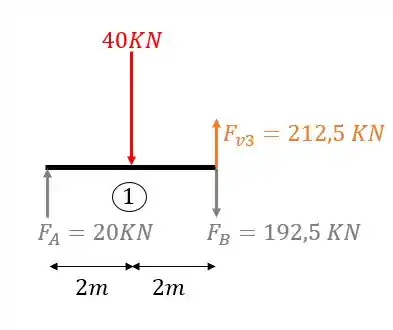
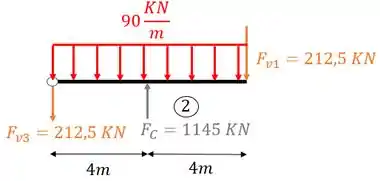
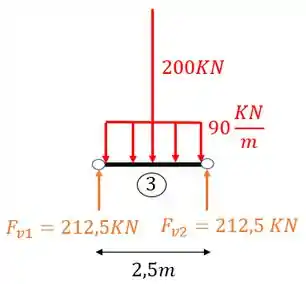
Veja que temos todos os dados pertinentes a todas as vigas, o que significa que a única coisa que falta sabermos são de fato os diagramas de cortante e momento fletor, sendo foco do exercício, apenas o diagrama de cortantes. Vamos lá então!
Passo 3
Antes de irmos para o cálculo das vigas, temos que lembrar como calculamos o diagrama e as equações do cortante, para isso, basta lembrar das fórmulas que usamos na aula de vigas simples, no assunto vigas mesmo, trazendo essas fórmulas aqui, e lembrando que nosso enfoque é apenas o cortante, teremos que primeiro definir uma equação para o nosso carregamento
Em seguida, usamos a seguinte equação para o cortante
- Cortante
- O primeiro é que deixa o cálculo muito mais simples
- E o segundo é porque deixa o cálculo muito mais simples kkkk
Lembrar que as condições de contorno sempre serão dadas pelas vigas. E outro ponto importante é: Para cada viga eu considero um novo referencial. Isso por dois motivos.
Ou seja, não coloca um referencial só e fica se matando pra fazer as contas, usa um referencial pra cada viga isoladamente e depois junta tudo, fica bem mais simples, agora chega de falar e vamos trabalhar.
Passo 4
Vamos calcular as equações de diagramas de cada viga.
- Viga 1
- Viga 2
- Viga 3
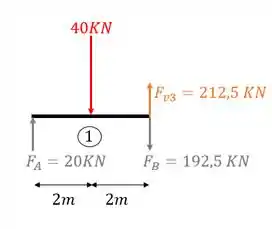
Sabemos que a primeira coisa que fazemos é definir o número de intervalos da nossa viga, e sabemos que esse numero é dado sempre que temos uma mudança brusca de carregamento. Como podemos ver, a carga concentrada de 40KN é o único carregamento ao longo da viga que causa uma mudança brusca de carregamento, logo, teremos dois intervalos nessa viga. Antes da carga de 40 e depois da carga de 40, vamos então calcular para o trecho antes do carregamento de 40 KN.
Como o nosso carregamento é concentrado, não há equação para o carregamento, que será dado por
Sabemos que a integral de zero é igual a constante, logo, podemos escrever nosso cortante como
Pelos dados da nossa viga sabemos que
Substituindo na nossa fórmula teremos
Logo temo que o cortante antes do carregamento de 40KN, é dado por
Fazendo para a região pós carregamento de 40KN teremos que
E o cortante é dado por
Porém a condição de contorno é dada por dois valores, um é o valor final do trecho anterior, que é dado por
Em que o menos representa antes da carga de 40KN, como queremos o próximo trecho, teremos que
Ou seja, agora estamos contabilizando ao último valor do trecho anterior, o valor do carregamento concentrado
Assim temos que
E podemos perceber que de fato o ultimo valor de cortante será negativo, visto que teremos que
Que também representa um cortante constante, assim teremos que o nosso diagrama de cortante da viga 1 será
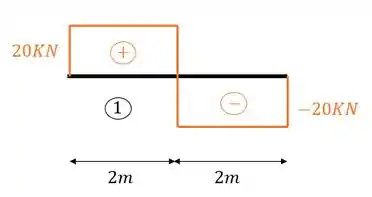
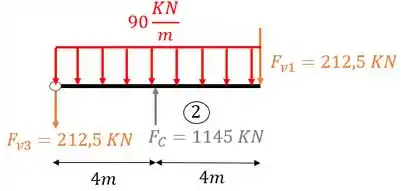
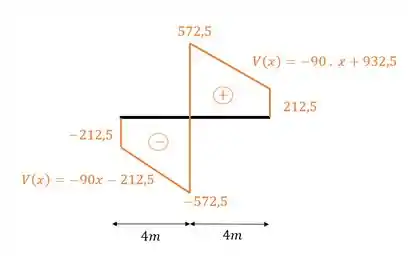
Sabemos que a primeira coisa que fazemos é definir o número de intervalos da nossa viga, e sabemos que esse número é dado sempre que temos uma mudança brusca de carregamento. Como podemos ver, a carga concentrada de 1145 KN é o único carregamento ao longo da viga que causa uma mudança brusca de carregamento, logo, teremos dois intervalos nessa viga. Antes da carga de 1145 e depois da carga de 1145, vamos então calcular para o trecho antes do carregamento de 1145 KN.
Como o nosso carregamento é distribuído, há equação para o carregamento, que será dado por
Sabemos que a integral será dada abaixo, logo, podemos escrever nosso cortante como
Pelos dados da nossa viga sabemos que
É perceba, que estamos usando um referencial diferente do anterior, já que novamente estamos considerando
Substituindo na nossa fórmula teremos
Logo temo que o cortante antes do carregamento de 1145KN, é dado por
Fazendo para a região pós carregamento de 1145KN teremos que
E o cortante é dado por
Porém a condição de contorno é dada por dois valores, um é o valor final do trecho anterior, que é dado por
Em que o menos representa antes da carga de 1145KN, como queremos o próximo trecho, teremos que
Ou seja, agora estamos contabilizando ao último valor do trecho anterior, o valor do carregamento concentrado
Assim temos que
Logo o cortante será dado por
Como podemos ver, tanto o trecho anterior, quanto o posterior são compostos de equações da reta decrescente, com isso, o nosso diagrama será dado por
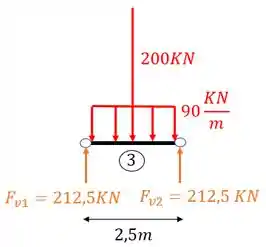
Sabemos que a primeira coisa que fazemos é definir o número de intervalos da nossa viga, e sabemos que esse número é dado sempre que temos uma mudança brusca de carregamento. Como podemos ver, a carga concentrada de 200 KN é o único carregamento ao longo da viga que causa uma mudança brusca de carregamento, logo, teremos dois intervalos nessa viga. Antes da carga de 200 e depois da carga de 200, vamos então calcular para o trecho antes do carregamento de 200 KN.
Como o nosso carregamento é distribuído, há equação para o carregamento, que será dado por
Sabemos que a integral será dada abaixo, logo, podemos escrever nosso cortante como
Pelos dados da nossa viga sabemos que
É perceba, que estamos usando um referencial diferente do anterior, já que novamente estamos considerando
Substituindo na nossa fórmula teremos
Logo temo que o cortante antes do carregamento de 1145KN, é dado por
Fazendo para a região pós carregamento de 200KN teremos que
E o cortante é dado por
Porém a condição de contorno é dada por dois valores, um é o valor final do trecho anterior, que é dado por
Em que o menos representa antes da carga de 200KN, como queremos o próximo trecho, teremos que
Ou seja, agora estamos contabilizando ao último valor do trecho anterior, o valor do carregamento concentrado
Assim temos que
Logo o cortante será dado por
Como podemos ver, tanto o trecho anterior, quanto o posterior são compostos de equações da reta decrescente, com isso, o nosso diagrama será dado por
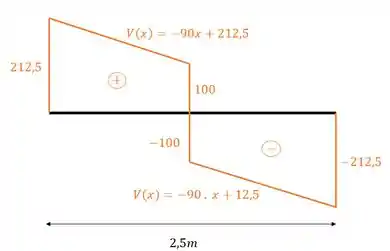
Passo 5
Agora vem uma parte bem importante, com tudo que calculamos até aqui, nós temos que o nosso diagrama é dado por
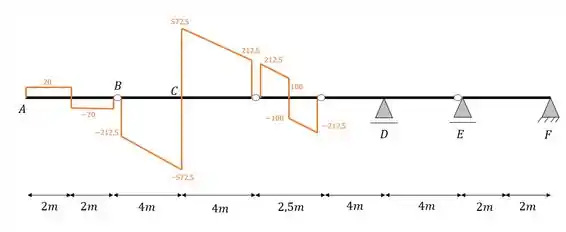
Como a nossa viga é simétrica, tudo que calculamos de cortante em um lado ocorre exatamente igual do outro, porém com o sentido invertido, como assim?
Por exemplo, vãos começar da última viga a direita.
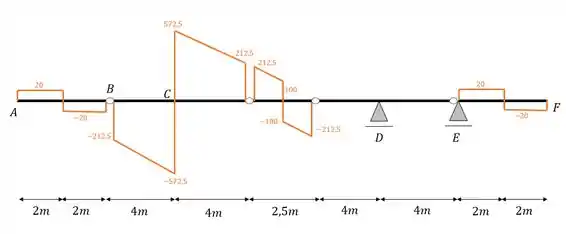
Perceba que o cortante começa ao contrário do que começou do lado esquerdo. Veja que do lado esquerdo começamos por cima, enquanto que do lado direito, por baixo, essa sequência inversa permanece até que as vigas se encontrem.
OBS: Perceba que os valores em módulos permanecem iguais pela simetria, porém, o sinal e o sentido se invertem, logo, tome muito cuidado com isso.
Prosseguindo no diagrama, teremos que
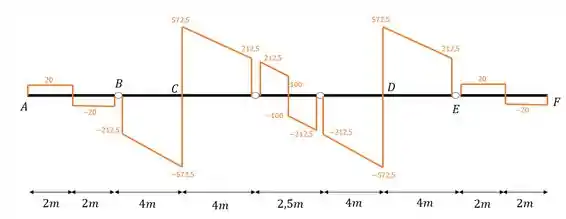
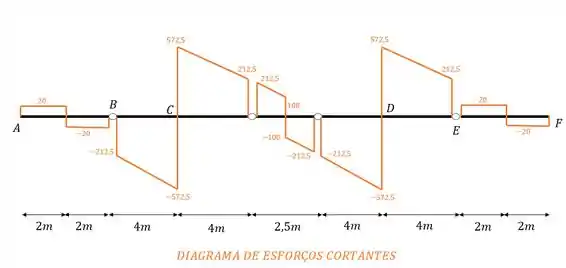
E esse será o diagrama completo de esforços cortantes da nossa viga Gerber. Bem trabalhoso mas agora já conseguimos pegar a manha do que devemos fazer. E assim terminamos de determinar o nosso diagrama, bora pro próximo exercício? Vamos lá então!!!!!
Resposta