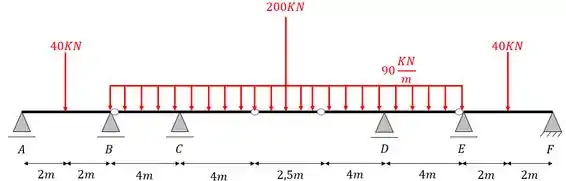
Na viga Gerber abaixo, determine todas as reações de apoio da viga, indicando o sentido das mesmas.
Passo 1
Como podemos ver se trata de um problema de viga Gerber. Nesse caso temos um passo a passo que nos auxilia a resolver esse tipo de problema de forma bem simples e direta. Esse tipo de questão sempre é muito trabalhosa, mas se seguirmos o passo a passo certinho ela sai bem rápido. O passo a passo é o seguinte.
- Primeiro quebramos as nossas rótulas e definimos apoios fictícios que sejam coerentes, ou seja, que tornem todas as vigas isostáticas e que também tenham um local para transferir a sua carga, já que se trata de um apoio fictício, ou seja, ele irá transferir a sua carga para algum lugar.
- Depois que tivermos todas as vigas isostáticas e com apoios fictícios, transferimos os seus carregamentos para as vigas respectivas e definimos uma ordem de solução para a nossa viga, começando sempre da viga mais externa e indo até a viga mais interna.
- Por fim, veja só, temos todas as vigas isostáticas, seus apoios fictícios, suas transferências e uma ordem de solução, agora é só começarmos a calcular as reações de apoio seguindo corretamente a ordem de solução definida.
- Em alguns exercícios a ultima parte seria definir os diagramas, porém nesse exercício iremos apenas até o cálculo das reações de apoios. Mas fique tranquilo pois teremos exercícios em que faremos o passo a passo com cálculo do diagrama.
Agora que já sabemos o passo a passo, vamos segui-lo e ir vendo como aplicar a solução em cada trecho, vamos lá???

Passo 2
Como vimos o nosso primeiro passo se trata de quebramos as rótulas e analisarmos onde colocaremos nossos apoios fictícios.
Quebrando as rótulas teremos os seguintes pontos de quebra
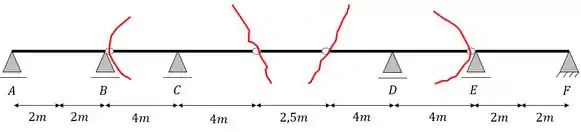
Separando as barras e numerando elas, teremos que

Agora como sabemos onde colocamos os apoios fictícios?
Basta olharmos as barras que não estão isostáticas (vale lembrar que no caso de vigas Gerber ignoramos forças horizontais, logo, mesmo que só haja reações verticais consideraremos isostática).
No nosso caso as barras isostáticas são as barras 1 e 5, logo, elas não precisam de apoios fictícios (vale lembrar que os apoios fictícios sempre entram nas rótulas quebradas). Porém é nítido que as barras 2,3,4 e 5 precisam de apoios para ficarem equilibradas, logo, serão elas quem receberão os apoios fictícios, e serão elas que se tornarão as vigas mais externas, como apresentamos na figura abaixo. Vale ressaltar que a viga 3 ainda se apoia nas vigas 2 e 4, o que torna ela uma viga ainda mais externa com relação as outras, visto que as vigas 2 e 4 só poderiam ser resolvidas com os valores das viga 3.
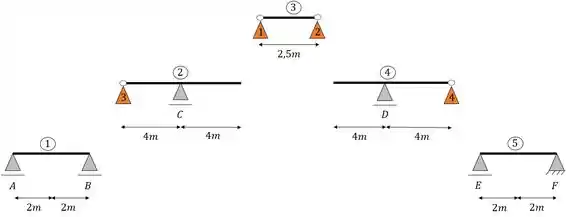
Para terminar esse passo só temos que indicar para onde transferiremos o carregamento dos apoios fictícios, dessa forma teremos.
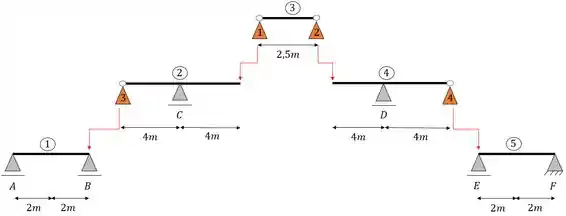
Vamos para o próximo passo agora.
Passo 3
O próximo passo é bem simples, agora que já temos os apoios fictícios e sua transferência, trocaremos o símbolo de apoio por forças e iremos indicar como, em que sentido e em qual local elas ficarão, e por fim indicaremos uma ordem de solução para o nosso problema.
Primeiro vamos trocar os apoios por vetores, e vamos fazer as transferências de carregamento. Fazendo isso teremos
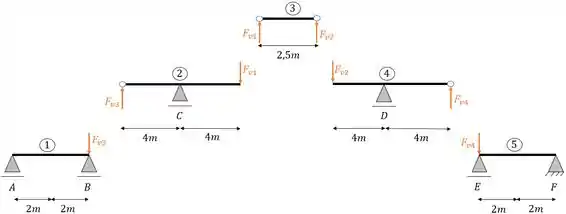
Veja que todas as reações de apoios fictícios são transferidas com sentidos opostos ao calculado, ou seja, o módulo permanece o mesmo, porém o sentido de ação é inverso, isso é muito importante na hora do cálculo.
Por fim, para terminarmos esse passo basta definirmos uma ordem de solução. Sempre começaremos palas vigas mais externas e depois iremos para as vigas mais internas, fazendo essa sequência, teremos que a nossa ordem de solução será dada por
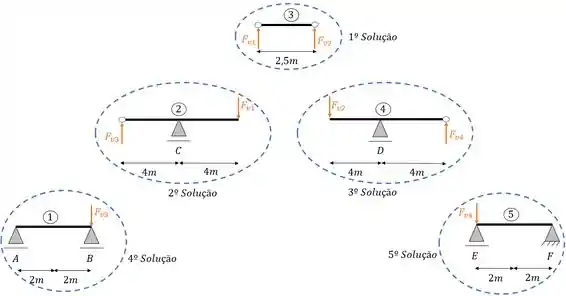
Só que aqui temos uma coisa legal, perceba que a nossa viga é simétrica, tanto em formato, quanto em carregamento (OBS: é muito importante a viga ser simétrica tanto em um quanto em outro para podermos fazer simetria, caso contrário temos que calcular tudo), sendo ela simétrica em ambos os casos, não precisamos calcular as reações de todas as vigas, mas apenas de um lado, e no fim, igualarmos os valores para os apoios simétricos. Dessa forma só precisamos calcular as seguintes vigas
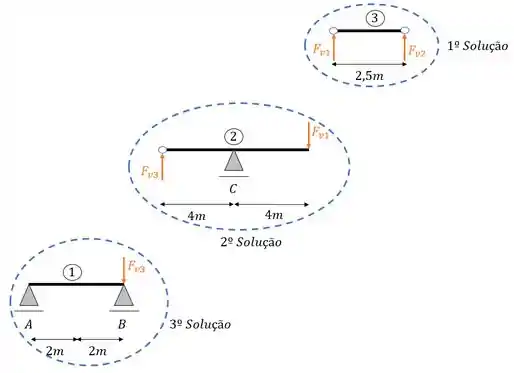
Bora para o último passo!!!
Passo 4
Agora que já fizemos os passos 1 e 2, vamos ao último passo do nosso exemplo, que será basicamente calcular reações de apoio, e basta que lembremos que, como em vigas Gerber nós menosprezamos forças horizontais, usaremos apenas somatório de forças verticais e somatório de momentos fletores. Vamos a nossa solução
- Reações viga 3
- Reações viga 2
- Reações viga 1
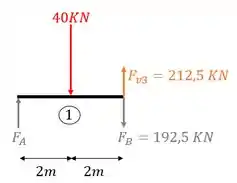
Perceba que na nossa ordem de solução não colocamos o carregamento, ou seja, precisamos por o carregamento dado no enunciado, e, a partir desse carregamento determinaremos as reações de apoio, com isso a nossa viga 3 será
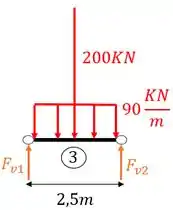
Calculando as reações de apoio teremos que
Calculadas as reações da viga 3, vamos para a sequência da solução que é a viga 2!!!
Perceba que na nossa ordem de solução não colocamos o carregamento, ou seja, precisamos por o carregamento dado no enunciado, e, a partir desse carregamento determinaremos as reações de apoio, com isso a nossa viga 2 será
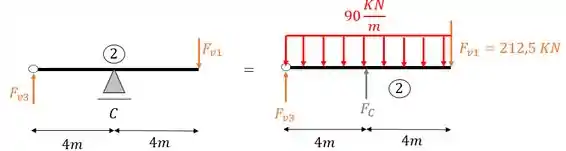
Calculando as reações de apoio teremos que
Como eu não gosto de trabalhar com valores negativos, eu inverto o vetor na nossa viga e mudo o sinal calculado, pois assim conseguimos sempre manter o cuidado com o sentido do nosso vetor calculado, dessa forma nossa viga passa a ser
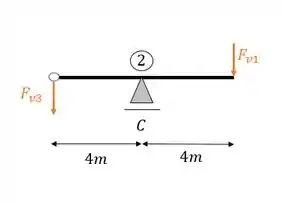
Assim quando transferirmos esse vetor para a ultima viga teremos que
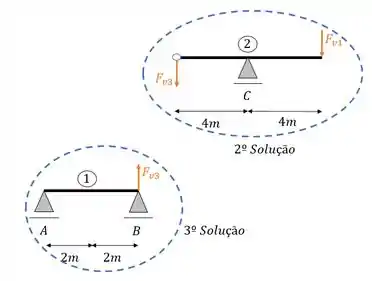
E nesse caso a nossa reação passa a ser
Calculadas as reações da viga 2, vamos para a sequência da solução que é a viga 1!!!
Perceba que na nossa ordem de solução não colocamos o carregamento, ou seja, precisamos por o carregamento dado no enunciado, e, a partir desse carregamento determinaremos as reações de apoio.
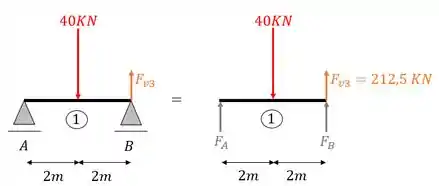
Calculando as reações de apoio teremos que
Como fizemos antes, vamos inverter o nosso vetor
Dessa forma podemos determinar as nossas reações de apoios por simetria, que serão dadas por
Agora acabamos o exercício, bora partir para o próximo!!!