Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Teorema Espectral

Ver Todos os Exercícios

Teoria

Fala aí, seja bem vindo ao Responde Aí! Bora conversar sobre Teorema Espectral?

O que diz o Teorema Espectral?

O Teorema Espectral nos dá uma forma mais rápida e mais prática de diagonalizar uma matriz! Ele nos diz que:

Seja uma matriz simétrica, então:

  • é diagonalizável;
  • Existe uma escolha de autovetores que formam uma base ortonormal em .

Beleza, agora vamos entender parte por parte desse teorema!

Matriz Simétrica

O teorema espectral é aplicado em matrizes simétricas. Mas afinal, quando uma matriz é simétrica?

Vamos considerar uma matriz qualquer, . A matriz é considerada simétrica quando , ou seja, quando os elementos fora da diagonal principal são simétricos. É como se a diagonal fosse um espelho! Saca só esse exemplo:

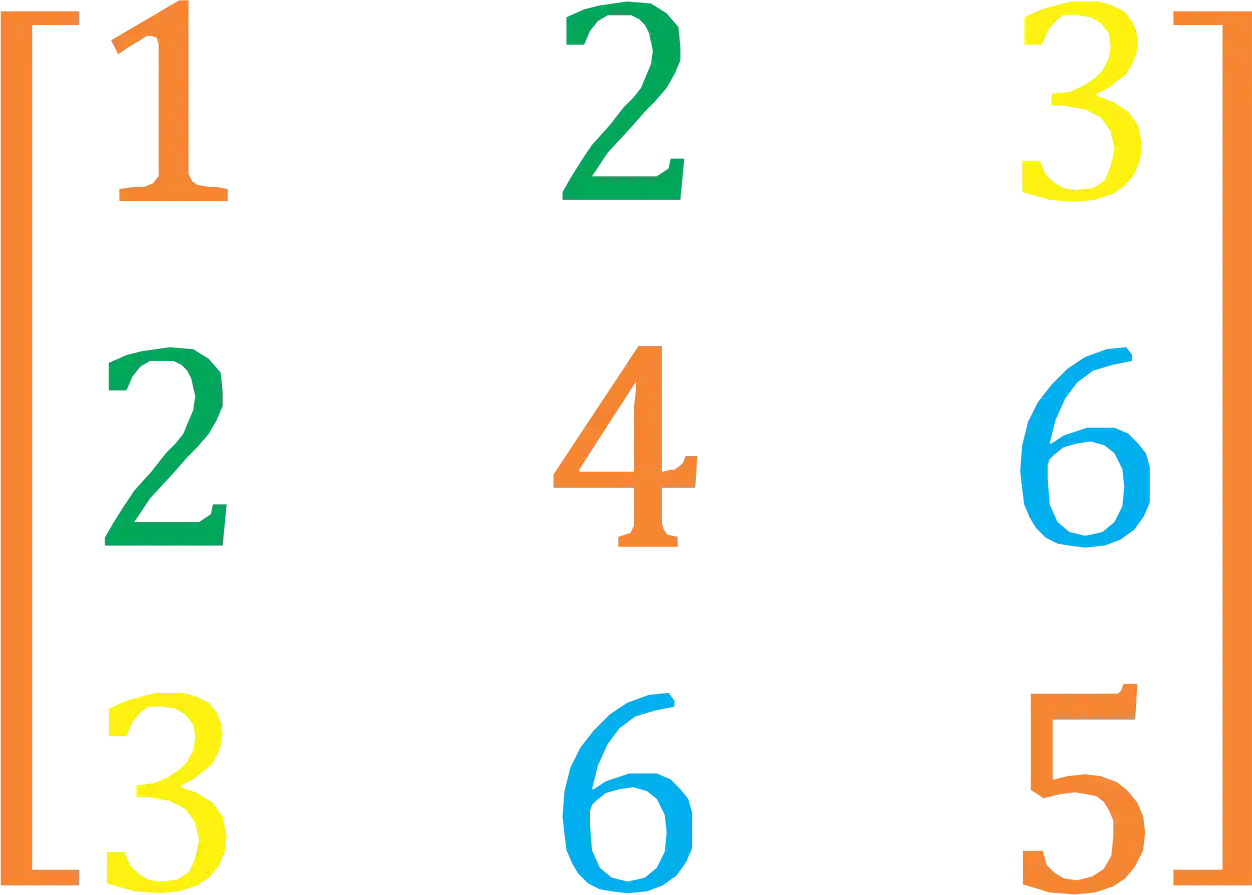
Matriz simétrica
Matriz simétrica

Qual é a Vantagem da Base Ortonormal?

A primeira parte do teorema fala que se for uma matriz simétrica então ela vai ser diagonalizável. O que já facilita a nossa vida! Mas em que autovetores que formam uma base ortonormal ajuda?

Quando vamos diagonalizar uma matriz, precisamos encontrar uma matriz e sua inversa certo? Mas calcular uma matriz inversa e complicado e trabalhoso… Mas se a matriz for composta por vetores ortonormais então ela seria uma matriz ortogonal!

E quando uma matriz é ortogonal a sua inversa é igual a sua transposta! 🤩🤩🤩

📢 Clique para ver mais:

Como usar o Teorema Espectral para a Diagonalização de Matrizes

Pra a gente aprender como usar o Teorema Espectral, vamos fazer um exemplo! Então considere a seguinte matriz :

Vamos verificar se é diagonalizável e achar as matrizes e

Passo 1: Verificar se a matriz é Simétrica

Essa é a parte mais fácil! Para saber se a matriz e simétrica, tudo que temos que fazer é escrever sua transposta:

Elas são iguais, portanto a matriz é simétrica e também diagonalizável!

Passo 2: Calcular os Autovalores de

Para isso consideramos:

Então:

Calculando os autovetores, temos:

Passo 3: Calcular os Autovetoes de

Primeiro vamos calcular os autovetores para :

Agora para :

Passo 4: Escrever e

Podemos definir nossa como:

Invertendo:

Prontinho!! Agora vamos praticar com mais exercícios?

Como usar o Teorema Espectral para a Diagonalização de Matrizes

Exercícios Resolvidos

Exercício Resolvido #1

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 318. – 14

Determinar uma matriz P que diagonaliza A ortogonalmente e calcular P - 1 A P .

a   A = 5 3 3 5

b   A = 0 0 2 0 - 1 0 2 0 0

Passo 1

a   Bom, o primeiro passo é achar os autovalores:

det ⁡ 5 - λ 3 3 5 - λ = 0

5 - λ 2 - 9 = 0

λ 2 - 10 λ + 16 = 0

Δ = 100 - 4 ∙ 1 ∙ 16

Δ = 100 - 64 = 36

λ = 10 ± 6 2 = 8   o u   2

Passo 2

Agora precisamos encontrar os autovetores:

λ = 8 :

- 3 3 3 - 3 x y = 0 0

- 3 x + 3 y = 0 ⇒ x = y 3 x - 3 y = 0 ⇒ x = y

Logo, o autoespaço associado é s p a n 1,1 .

λ = 2 :

3 3 3 3 x y = 0 0

3 x + 3 y = 0 ⇒ x = - y 3 x + 3 y = 0 ⇒ x = - y

Logo o autoespaço associado é s p a n 1 , - 1

Passo 3

Ele quer uma matriz P que diagonaliza A ortogonalmente. Ou seja, ele quer que P seja ortogonal (possua colunas ortonormais). Como os vetores que obtivemos 1,1 e 1 , - 1 já são ortogonais, temos apenas que normalizá-los. Logo:

1,1 1,1 = 1,1 2 = 1 2 , 1 2

1 , - 1 1 , - 1 = 1 , - 1 2 = 1 2 , - 1 2

Podemos então escrever nossa matriz P como:

P = 1 2 1 2 1 2 - 1 2

Passo 4

Por fim, poderíamos calcular P - 1 A P , que nesse caso seria equivalente a P T A P já que P é ortogonal. No entanto, sabemos que essa é uma matriz diagonal com os autovalores de A . Autovalores esses que já calculamos! Então, obedecendo à ordem que escolhemos para os autovetores em P , temos:

P - 1 A P = 8 0 0 2

Passo 5

b   Novamente, achamos os autovalores:

det ⁡ 0 - λ 0 2 0 - 1 - λ 0 2 0 0 - λ = 0

0 - λ - 1 - λ 0 - λ - 4 - 1 - λ = 0

λ 2 - 1 - λ - 4 - 1 - λ = 0

λ 2 - 4 - 1 - λ = 0

λ - 2 λ + 2 - 1 - λ = 0

Beleza, temos então três autovalores λ = 2 , λ = - 2 e λ = - 1 .

Passo 6

Agora precisamos encontrar os autovetores:

λ = 2 :

- 2 0 2 0 - 3 0 2 0 - 2 x y z = 0 0 0

- 2 x + 2 z = 0 ⇒ x = z - 3 y = 0 ⇒ y = 0 2 x - 2 z = 0

Logo, o autoespaço associado é s p a n 1,0 , 1 .

λ = - 2 :

2 0 2 0 1 0 2 0 2 x y z = 0 0 0

2 x + 2 z = 0 ⇒ x = - z y = 0 ⇒ y = 0 2 x + 2 z = 0

Logo o autoespaço associado é s p a n 1,0 , - 1

λ = - 1 :

1 0 2 0 0 0 2 0 1 x y z = 0 0 0

x + 2 z = 0 ⇒ x = - 2 z 2 x + z = 0 ⇒ x = - z 2

Temos então que:

- 2 z = - z 2 ⇒ z = 0 ⇒ x = 0

Como não temos nenhuma condição para y ele pode assumir qualquer valor!

Logo o autoespaço associado é s p a n 0,1 , 0

Passo 7

Novamente temos vetores ortogonais, mas ainda precisamos normalizá-los! Logo:

1,0 , 1 1,0 , 1 = 1,0 , 1 2 = 1 2 , 0 , 1 2

1,0 , - 1 1,0 , - 1 = 1,0 , - 1 2 = 1 2 , 0 , - 1 2

Podemos então escrever nossa matriz P como:

P = 1 2 0 1 2 0 1 0 1 2 0 - 1 2

Passo 8

Por fim, poderíamos calcular P - 1 A P , que nesse caso seria equivalente a P T A P já que P é ortogonal. No entanto, sabemos que essa é uma matriz diagonal com os autovalores de A . Autovalores esses que já calculamos! Então, obedecendo à ordem que escolhemos para os autovetores em P , temos:

P - 1 A P = 2 0 0 0 - 1 0 0 0 - 2

Resposta

a   P = 1 2 1 2 1 2 - 1 2 e P - 1 A P = 8 0 0 2

b   P = 1 2 0 1 2 0 1 0 1 2 0 - 1 2 e P - 1 A P = 2 0 0 0 - 1 0 0 0 - 2

Exercício Resolvido #2

Lista 1 para a P3, exercício 15-a)-b), Álgebra Linear I, PUC-rio, Adaptado.

Seja A = 1 - 1 - 1 1

a   Determine de A é diagonalizável.

b   Se ela for, apresente uma P e P - 1 que satisfaça a diagonalização.

Considere:

A = P D P - 1

Passo 1

a   Bom, existem dois jeitos de fazer essa questão. Um deles é o no pau e pedra e achar os autovetores e verificar se existe ou não uma base de autovetores. Nesse caso, você teria que achar o domínio da transformação que representa essa A .

Por outro lado, podemos ver que a matriz A é simétrica, e pelo teorema espectral sabemos que ela é diagonalizável.

Passo 2

b   Um jeito fácil e rápido para montar a nossa P e P - 1 é usar o teorema espectral. Por que se a nossa P for ortogonal, teremos P - 1 = P T . No entanto como estamos trabalhando com matrizes 2 × 2 , inverter a matriz fica bem fácil! É só fazer isso oh:

A = a b c d

A - 1 = 1 det ⁡ A d - b - c a

Então primeiro vamos calcular os autovalores.

A - λ I = 1 - λ - 1 - 1 1 - λ ⇒

det ⁡ A - λ I = p λ = 1 - λ 2 - 1

1 - λ 2 - 1 = 0 ⇒   1 - λ 2 = 1 ⇒

1 - λ = ± 1 ⇒

λ = 0 ou λ = 2

Passo 3

Vamos calcular os autovetores para λ = 0 :

1 - 1 - 1 1 x y = 0

x - y = 0 ⇒ x = y - x + y = 0

x , x = x 1,1 ⇒

V λ = 0 = s p a n 1,1

Para λ = 2 :

- 1 - 1 - 1 - 1 x y = 0

- x - y = 0 ⇒ x = - y

- y , y = y - 1,1

V λ = 2 = s p a n - 1,1

Passo 4

Então podemos definir nossa P como:

P = 1 - 1 1 1

Invertendo:

P - 1 = 1 2 1 1 - 1 1 = 1 2 1 2 - 1 2 1 2

Agora pra ver se se satisfaz é só multiplicar:

A = P D P - 1 ⇒ D = P - 1 A P

D = 1 2 1 2 - 1 2 1 2 ⋅ 1 - 1 - 1 1 ⋅ 1 - 1 1 1

D = 0 0 - 1 1 ⋅ 1 - 1 1 1

D = 0 0 0 2

Resposta

a Sim, pois A é simétrica.

b P = 1 - 1 1 1 e P - 1 = 1 2 1 2 - 1 2 1 2

Exercício Resolvido #3

PUCRIO-P3-2014.2-2d

Para cada k real, considere a transformação T : R 3 ⟶ R 3 dada por:

T x , y , z = k x + 2 y ,   2 x + k y + 2 z ,   2 y + k z

Existe um valor de k para qual T não seja diagonalizável?

Passo 1

Não, pois como podemos observar a matriz abaixo em função de k :

T ε = k 2 0 2 k 2 0 2 k

A matriz acima é sempre simétrica independente do valor de k e, por isso, de acordo com o teorema espectral, é diagonalizável.

Também sabemos que se uma representação de T em uma base for diagonalizável, todas as outras serão e, portanto, T é diagonalizável.

Logo, não existe nenhum valor para k , tal que, T não seja diagonalizável.

Resposta

Não existe.

Exercício Resolvido #4

PUCRIO-P3-2015.1-2bc

Considere T : R 3 ⟶ R 3 dada por T x , y , z = x , y , z × 0 , a , 0 + ( 2 x + 2 a z , a y , 2 z ) , onde a ∈ R . Denotamos por ε a base canônica de R 3 .

a   Calcule a matriz T ε ← ε e determine se T é diagonalizável para qualquer valor a ∈ R . (Dica: não tente calcular os autovetores)

b   No caso em que a = 2 , ache uma base de R 3 constituída de autovetores de T .

Passo 1

a   Bom, para começar vamos construir a matriz antes de tudo.

T 1,0 , 0 = 1,0 , 0 × 0 , a , 0 + ( 2,0 , 0 )

T 0,1 , 0 = 0,1 , 0 × 0 , a , 0 + 0 , a , 0

T 0,0 , 1 = 0,0 , 1 × 0 , a , 0 + ( 2 a , 0,2 )

Calculando os produtos vetoriais:

1,0 , 0 × 0 , a , 0 = i j k 1 0 0 0 a 0 = a k = ( 0,0 , a )

0,1 , 0 × 0 , a , 0 = i j k 0 1 0 0 a 0 = 0,0 , 0

0,0 , 1 × 0 , a , 0 = i j k 0 0 1 0 a 0 = - a i = - a , 0,0

Passo 2

E assim:

T 1,0 , 0 = 0,0 , a + 2,0 , 0 = ( 2,0 , a )

T 0,1 , 0 = 0,0 , 0 + 0 , a , 0 = ( 0 , a , 0 )

T 0,0 , 1 = - a , 0,0 + 2 a , 0,2 = ( a , 0,2 )

Calculando a matriz:

T ε = 2 0 a 0 a 0 a 0 2

Como podemos ver a matriz é simétrica, então de acordo com o teorema espectral, a matriz é diagonalizável, então todas as outras representações também são, e portanto, T é diagonalizável.

Passo 3

b   Agora substituindo a = 2 na matriz:

T ε = 2 0 2 0 2 0 2 0 2

Agora para achar os autovalores:

T ε - λ I = 2 - λ 0 2 0 2 - λ 0 2 0 2 - λ

det ⁡ T ε - λ I = 2 - λ 3 - 4 2 - λ = 0 ⇒

2 - λ 2 - λ 2 - 4 = 0

2 - λ = 0 ⇒ λ = 2

o u

2 - λ 2 - 4 = 0 ⇒ 2 - λ 2 = 4 ⇒ 2 - λ = ± 2

λ = 0   o u   λ = 4

Passo 4

Para achar os autovetores:

Para λ = 2 :

0 0 2 0 0 0 2 0 0 x y z = 0 ⇒

2 z = 0 ⇒ z = 0 0 = 0 2 x = 0 ⇒ x = 0

Sabemos que x = z = 0 , mas y pode ser qualquer coisa!!

0 , y , 0 = y 0,1 , 0 ∴

V λ = 2 = s p a n 0,1 , 0

Para λ = 0 :

2 0 2 0 2 0 2 0 2 x y z = 0 ⇒

2 x + 2 z = 0 ⇒ x = - z 2 y = 0 ⇒ y = 0 2 x + 2 z = 0

x , y , z = - z , 0 , z = z - 1,0 , 1

V λ = 0 = s p a n - 1,0 , 1

Para λ = 4

- 2 0 2 0 - 2 0 2 0 - 2 x y z = 0 ⇒

- 2 x + 2 z = 0 ⇒ x = z - 2 y = 0 ⇒ y = 0 2 x - 2 z = 0

x , y , z = z , 0 , z = z 1,0 , 1

V λ = 4 = s p a n { 1,0 , 1 }

Assim uma possível base α de R 3 pode ser:

α = 1,0 , 1 , - 1,0 , 1 , 0,1 , 0

Resposta

a   É diagonalizável.

b   Uma possível base de R 3 é: α = 1 , 0,1 , - 1,0 , 1 , 0,1 , 0

Exercícios de Livros Relacionados

1. Em cada parte, encontre a decomposição espectral da matriz(a) 3 1 1 3 (b) 6 - 2 - 2 3 (c) - 3 1 2 1 - 3 2 2 2 0 (d) - 2 0 - 36 0 - 3 0 - 36 0 - 23
1. Em cada parte, encontre a decomposição espectral da matriz(a) 3 1 1 3 (b) 6 - 2 - 2 3 (c) - 3 1 2 1 - 3 2 2 2 0 (d) - 2 0 - 36 0 - 3 0 - 36 0 - 23
Seja A ∈ L( R 3 ) o operador linear cuja matriz relativa à base canônica é ( a i j ) = 2 2 0 2 - 1 0 0 0 2 a) Achar os valores próprios de A. b) Achar uma matriz ortonormal do R 3 em relação à qual a