Diagonalização
Teoria
Fala aí! Bora aprender TUDO sobre Diagonalização de Matrizes?
O que Significa Diagonalizar uma Matriz?
Diagonalizar é escrever uma matriz, que representa uma transformação linear (TL) na base dos autovetores na qual ela é diagonal.
-Hãam? 😖
Pra ficar mais claro eu vou te dar um exemplo!
Vamos pegar uma
O que fizemos aqui foi pegar uma matriz
Agora você me pergunta, qual é a relação entre a matriz
O que é uma excelente pergunta! Os elementos da diagonal da matriz
Dizemos que uma matriz
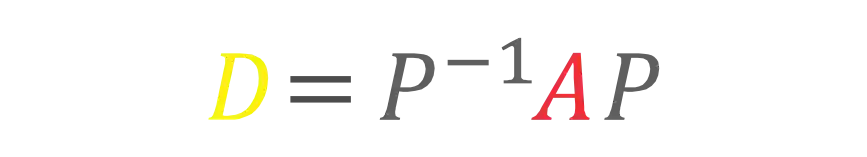
Essa matriz
Uma outra forma de escrever a relação acima é essa daqui:
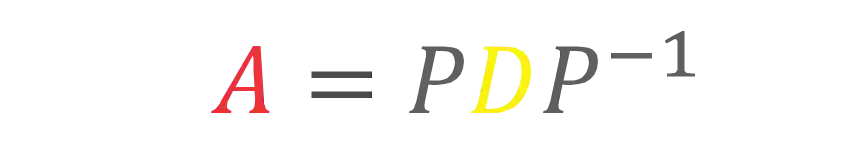
Chamamos essa relação de decomposição espectral, guarda esse nome porque ele é importante! Mas agora vamos ao que interessa…bora aprender o passo a passo pra diagonalizar uma matriz e é claro, como descobrir se uma matriz é diagonalizavel!
Como Diagonalizar uma Matriz?
Pra a gente aprender como diagonalizar uma matriz, vamos usar o mesmo exemplo que vimos ali em cima e calcular
A resolução desse problema você também pode conferir no vídeo abaixo!
Passo 1: Calcular os Autovalores de
Pra a gente achar a forma diagonal da matriz
A matriz
Fazendo isso, temos:
Passo 2: Calcular os Autovetores
Para calcular os autovetores, fazemos:
Primeiro calculamos o autovetor associado a
Agora, para o autovetor associado a
Passo 3: Montar a Matriz D e a Matriz P
Finalmente podemos montar a matriz diagonal
Prontinho!
Exercícios Resolvidos
Exercício Resolvido #1
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 210 – Fix 7.15
A matriz abaixo está fatorada na forma . Sem fazer contas, determine os autovalores da matriz e bases para cada um dos autoespaços.
Passo 1
Como vimos nesse capítulo, ao fatorarmos uma matriz na forma:
Com matriz diagonal, temos que a diagonal de são os autovalores dessa matriz, e as colunas de são autovetores associados aos autovalores (na ordem em que eles aparecem em ). E é exatamente essa fatoração que o enunciado nos dá!
Sendo assim, temos o autovalor associado ao autoespaço . Uma base para ele são os próprios autovetores .
Já o autovalor está associado ao autoespaço que tem como base .
Resposta
Autovalor associado ao autoespaço com base .
Autovalor associado ao autoespaço com base .
Exercício Resolvido #2
Elaboração Própria
Diga se a matriz abaixo é diagonalizável:
Passo 1
Fazendo :
Temos:
Passo 2
Para :
Então o autoespaço associado é , ou seja, .
Passo 3
Para :
Então temos e, portanto, .
Logo
Como e são , então temos uma base de autovetores, se considerarmos uma matriz que representa uma .
Logo a matriz é diagonalizável.
Resposta
É diagonalizável.
Exercício Resolvido #3
Lista 1 para a P3, exercício 12-a)-b), Álgebra Linear I, PUC-rio.
Seja dada por:
Encontre os autovalores de e os respectivos autoespaços.
A transformação é diagonalizável? Se sim, dê sua forma diagonal.
Passo 1
Para encontrar os autovalores precisamos passar a transformação para uma forma matricial, assim vamos escolher a mais fácil, , sendo .
Assim temos que:
Passo 2
Para calcular os autovalores vamos fazer
Assim temos que:
E o polinômio característico é:
Ou
Passo 3
Para calcular os autovetores:
Logo quem é nosso autovetor?
Cuidado! Não é o vetor nulo só porque .
E o autoespaço é:
Passo 4
Assim, podemos afirmar que nossa não é diagonalizável, porque não existe uma base de autovetores para o seu domínio.
Resposta
não é diagonalizável, porque não existe uma base de autovetores para o seu domínio.
Exercício Resolvido #4
Curso de Álgebra Linear, Fundamentos e Aplicações Terceira Edição, Marco Cabral e Paulo Golfeld, página 211 Prob. 7.12
Considere . Determine e tais que:
Passo 1
A questão nos pede para escrevermos matrizes de acordo com as equações. E o que essas equações te lembram?
Diagonalização!! Isso mesmo, então sabemos que é diagonalizável e ele quer que a gente descubra as matrizes dos autovetores que faltam! Mas tem uma diferença entre as duas letras. Repare que a ordem nas diagonais estão trocadas, isso também altera a ordem dos autovetores. Sendo assim, vamos aos cálculos!
Passo 2
Sabendo que temos dois autovalores diferentes, calculá-los:
Para :
Bom assim, temos que nosso autoespaço será:
E assim:
E já era de se esperar que a dimensão fosse , já que o autovalor se repete duas vezes.
Para :
E assim:
Passo 3
Agora já podemos montar nossa matriz de autovetores! Como o autovalor vem primeiro na matriz diagonal:
Passo 4
Aqui vamos usar o mesmo procedimento da letra , como já sabemos os autovetores basta seguir a ordem da matriz diagonal e como ordem dos autovalores é :
OBS: A ordem dos autovetores associados ao não importa.
Resposta