Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Coordenadas Polares

Ver Todos os Exercícios

Teoria

Desde o colégio usamos o sistema cartesiano. Assim, para localizar um ponto precisamos do valor das coordenadas x ,   y e z . Mas, se tivermos o gráfico a seguir como faremos para localizar o ponto P ?

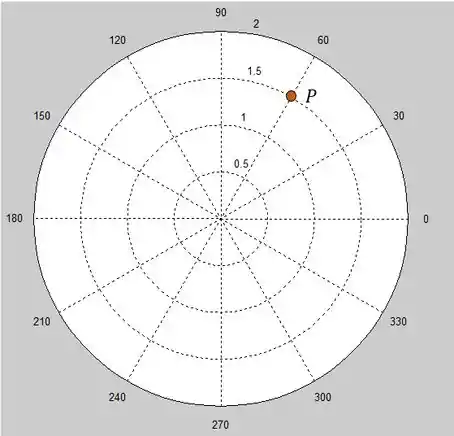
Não faço ideia de como localizar o ponto!! E nunca vi essa representação antes!!

Calma!! Vamos te ensinar tudo o que precisas saber para localizar o ponto certinho!! Blz?!

Para conseguirmos identificar o ponto P da figura teremos que utilizar as coordenadas polares. Mas, quais são essas coordenadas?

Hahaha! Não são bem essas aí não!

Vou mostrar como a gente encontra elas (de verdade)!

Bem, para localizar um ponto por meio das coordenadas polares precisamos saber qual a distância desse ponto até a origem e também precisamos saber o ângulo entre a reta que o ponto forma com a origem e o eixo polar. Não entendi nada!! Vamos analisar então uma outra figura!!

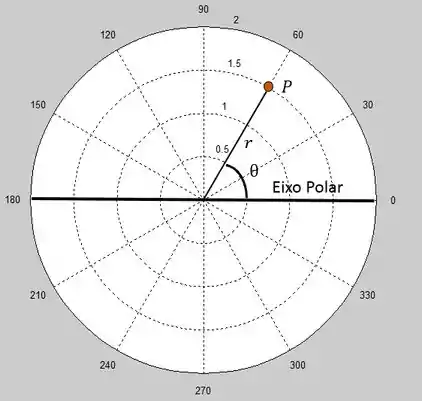
A reta que liga o ponto P ao centro possui um comprimento r que pela figura vemos que vale 1.5 , então esse valor é a distância do ponto P até a origem. O ângulo que precisamos saber está também indicado na figura, e que equivale a θ = 60 ° . Como você pode observar o círculo mais externo possui o valor dos ângulos formados pelas linhas, então, por meio deles conseguimos o ângulo que queremos. Assim, nosso ponto P = ( 1.5 ,   60 ° ) . Pronto, achamos as coordenadas do nosso ponto!

Agora que já entendemos como faz, podemos colocar para um caso genérico!!

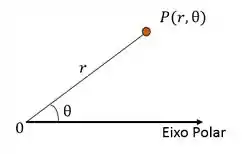
Obs: O r é um valor positivo, mas ele pode aparecer como ( - r , θ ) , essa representação é equivalente à ( r ,   θ + π ) . Assim, ( - r , θ ) é o simétrico de ( r , θ ) em relação ao polo.

Já sabemos as coordenadas polares!! Mas, e se eu estiver no sistema cartesiano e quiser passar para coordenadas polares, ou vice e versa?! Vamos ver isso agora!!

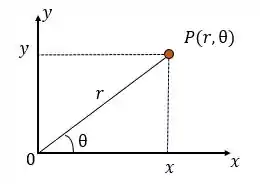
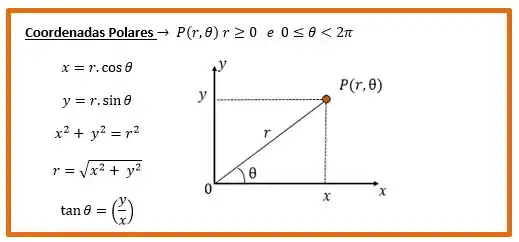
Para passar de um sistema para outro devemos ter sempre a figura acima em mente!!

Na figura temos os dois sistemas juntos, ou seja, a representação cartesiana x e y e a representação polar por meio de r e θ . Da figura, conseguimos tirar as seguintes relações:

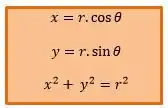
Assim, por meio delas conseguimos passar de polar para cartesiana, e o contrário é só rearranjar as relações e teremos:

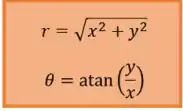
Agora sim!! Sabemos tudo o que precisamos saber de coordenadas polares!! Lembre-se: tudo o que você precisa saber sobre coordenadas polares você consegue olhando para a figura acima e observando as relações entre x ,   y ,   r e θ .

Um resuminho para tus

Agora é só partir para o exercício!

Exercícios Resolvidos

Exercício Resolvido #1

Elaboração Própria

Apresentar as equações em coordenadas polares:

  1. Das retas x = a , x = - a , y = a e y = - a sendo a = c o n s t a n t e
  2. Da circunferência de centro no pólo e raio a > 0
  3. Da circunferência de centro ( x 0 ,   y 0 ) e raio a > 0

Passo 1

Neste exercício temos que passar as equações de coordenadas cartesianas para polares. Para isso, vamos utilizar as seguintes relações que vimos na teoria:

x = r . cos ⁡ θ               ( 1 )

y = r . sin ⁡ θ               ( 2 )

x 2 +   y 2 = r 2       ( 3 )

Bora colocar a mão na massa!! ;)

Passo 2

a) Nesse item devemos escrever as equações das retas x = a , x = - a , y = a e y = - a em coordenadas polares. Vamos começar com a reta x = a .

Para x = a vamos substituir a expressão ( 1 )

x = a →   r . cos ⁡ θ = a

Como a é uma constante então achamos a expressão da reta em coordenadas polares:

r . cos ⁡ θ = a

Agora, para x = - a , o procedimento é o mesmo e atente que o que muda para a expressão anterior é o sinal de menos no a , então a expressão ficará no lado esquerdo igual e no lado direito com - a .

r . cos ⁡ θ = - a

Para y = a , agora, vamos utilizar a expressão ( 2 ) . Substituindo, temos:

y = a → r . sin ⁡ θ = a  

E para terminar esse item, para y = - a , teremos a expressão acima, mas com o lado direito com - a .

r . sin ⁡ θ = - a  

Passo 3

b) Devemos escrever em coordenadas polares a expressão da circunferência de centro no pólo e raio a > 0 .

Centro no pólo é o mesmo que dizer que o centro está na origem, assim, sabemos que C ( 0 ,   0 ) . E, pelo enunciado o raio é a . Quando vimos cônicas degeneradas e mesmo no colégio vimos que a equação geral de uma circunferência é:

x - x 0 2 + y - y 0 2 = r 2

Sendo, x 0 ,   y 0 as coordenadas do centro da esfera e r o raio. CUIDADO: O r na expressão acima representa o raio da esfera e não é o mesmo r das coordenadas polares.

Assim, nossa esfera em coordenadas cartesianas fica:

x 2 + y 2 = a 2

Para passar para as coordenadas polares vamos utilizar expressão ( 3 ) , então teremos:

r 2 = a 2

Uhulll!! Mais um item pronto!!

Passo 4

c) Para terminar vamos escrever a expressão em coordenadas polares da circunferência de centro ( x 0 ,   y 0 ) e raio a > 0 .

No item anterior vimos que a expressão geral em coordenadas cartesianas de uma circunferência é:

x - x 0 2 + y - y 0 2 = r 2

Sendo, x 0 ,   y 0 as coordenadas do centro da esfera e r o raio. Substituindo as informações que temos:

x - x 0 2 + y - y 0 2 = a 2

Agora, devemos usar as relações 1 ,   ( 2 ) e ( 3 ) para achar a equação em coordenadas polares:

x 2 - 2 x x 0 + x 0 2 + y 2 - 2 y y 0 + y 0 2 = a 2

Substituindo as relações temos que:

r 2 - 2 r . cos ⁡ θ . x 0 +     x 0 2 - 2 r . sin ⁡ θ . y 0 + y 0 2 =   a 2

Pronto chegamos na nossa expressão, lembrando que x 0 ,   y 0 e a são constantes.

Resposta

a )     x = a → r . cos ⁡ θ = a , x = - a → r . cos ⁡ θ = - a , y = a → r . sin ⁡ θ = a ,

y = - a → r . sin ⁡ θ = - a

b )     r 2 = a 2

c )   r 2 - 2 r . cos ⁡ θ . x 0 +     x 0 2 - 2 r . sin ⁡ θ . y 0 + y 0 2 =   a 2

Exercício Resolvido #2

Unicamp, 2ª Chamada – Geometria Analítica, 20/06/2013 (manhã), pág. 1, Questão 5 – item c.

Verificar se as afirmações abaixo são verdadeiras ou falsas. (Respostas sem justificativa não serão consideradas)

c) A equação (em coordenadas polares) r = - 4 cos ⁡ θ representa uma parábola.

Passo 1

O exercício faz uma afirmação em relação à expressão r = - 4 cos ⁡ θ que está em coordenadas polares. Ele afirma que a expressão representa uma parábola. Será que isso é verdade?

Para verificar, vamos passar para as coordenadas cartesianas e verificar!! Blz?

Passo 2

Como a expressão está escrita em coordenadas polares e queremos passar para as coordenadas cartesianas vamos utilizar as seguintes relações:

x 2 +   y 2 = r 2 → r = x 2 +   y 2   ( 1 )

x = r . cos ⁡ θ → cos ⁡ θ = x x 2 +   y 2   ( 2 )

y = r . sin ⁡ θ → sin ⁡ θ = y x 2 +   y 2   ( 3 )

Substituindo as relações, temos:

r = - 4 cos ⁡ θ →   x 2 +   y 2 = - 4 x x 2 +   y 2  

Escrevendo de um jeito diferente a expressão acima, temos:

x 2 +   y 2 = - 4 x

( x + 2 ) 2 + y 2 = 4

Essa é a expressão de uma circunferência de raio 2 e centro ( - 2 ,   0 ) .

Portanto, a afirmativa é FALSA. A nossa justificativa é o próprio desenvolvimento para achar a expressão!!

Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #3

Elaboração Própria

Represente graficamente as regiões descritas em coordenadas polares:

  1. 0 ≤ r ≤ 1 e 0 ≤   θ ≤   π b) 1 ≤ r ≤ 2 e 0 ≤   θ ≤ π 2

Passo 1

Esse exercício é um pouco diferente do que vínhamos fazendo!! Agora, não precisamos passar de polares para cartesianas, mas representar a região descrita pelas coordenadas polares.

Passo 2

a) 0 ≤ r ≤ 1 e 0 ≤   θ ≤   π

Nosso r vai de 0 até 1 e nosso ângulo vai de 0 ° até 180 ° . Então, se desenharmos teríamos a seguinte figura:

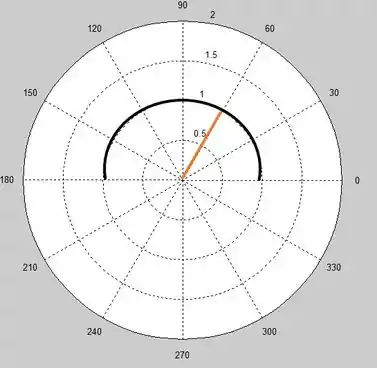
A reta laranja representa o nosso r que vai de 0 até 1 . O arco em preto representa a restrição em relação ao nosso ângulo θ . Então juntado as duas informações sobre r e θ , teremos a seguinte figura:

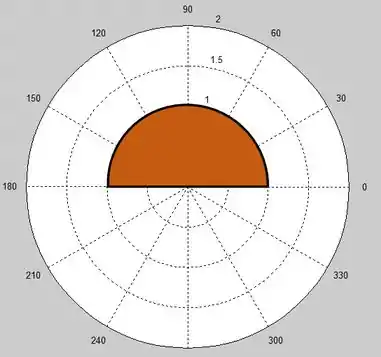
Pronto!! Chegamos na região que as coordenadas polares dadas pelo enunciado representam!!

Passo 3

b)   1 ≤ r ≤ 2 e 0 ≤   θ ≤ π 2

Vamos fazer o mesmo procedimento do item anterior. Agora, nosso r vai de 1 até 2 , e nosso

ângulo vai de 0 ° até 90 ° .

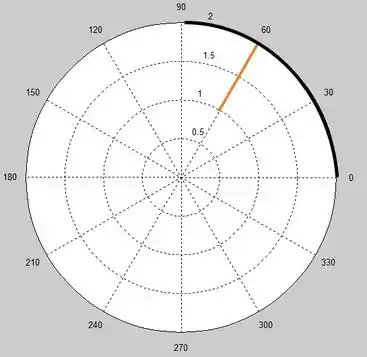
A reta laranja representa o r e o arco em preto representa nosso ângulo. Juntando r e θ , temos:

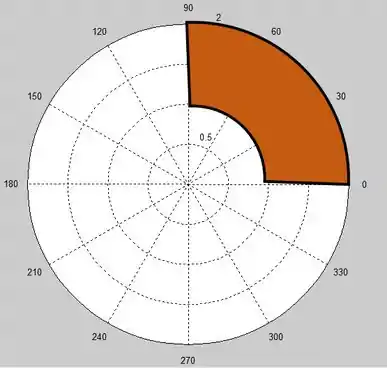
Resposta

Ei, a resposta está no passo a passo :)

Exercício Resolvido #4

Unicamp, P3 – Geometria Analítica, 01/07/2009, Professor Marcelo M. Santos, pág. 1, Questão 1-item a

Identifique a cônica dada em coordenadas polares, determine a sua equação em coordenadas cartesianas e faça um esboço do seu gráfico:

  r = 6 3 + sin ⁡ θ

Passo 1

Vamos lá!! O enunciado nos dá uma equação em coordenada polares e a partir dela devemos identificar qual cônica a expressão representa. Além disso, devemos passar a equação para o sistema cartesiano e fazer um esboço do seu gráfico. Bora, começar então?!

Passo 2

                              r = 6 3 + sin ⁡ θ

Bora lá!

Usando as relações,

1   r = x 2 + y 2

2   x = r . cos ⁡ θ

3   y = r . sin ⁡ θ

Vamos encontrar a equação cartesiana da expressão dada em coordenadas polares:

r = 6 3 + sin ⁡ θ →   x 2 +   y 2 = 6 3 + sin ⁡ θ   ( 4 )

Da expressão ( 3 ) , temos que y = r sin ⁡ θ , que podemos escrever:

sin ⁡ θ = y x 2 +   y 2   ( 5 )

Substituindo ( 5 ) em ( 4 ) , temos:

x 2 +   y 2 = 6 3 + y x 2 +   y 2

Reescrevendo, temos:

x 2 +   y 2   =   6 3 + y x 2 +   y 2

x 2 +   y 2   =   6 x 2 +   y 2 3 x 2 +   y 2 + y

Como os dois lados da equação estão multiplicados por x 2 +   y 2 , podemos cortá-los! Assim,

1   =   6 3 x 2 +   y 2 + y

3 x 2 +   y 2 + y = 6

x 2 +   y 2 = 6 - y 3

Elevando os dois lados ao quadrado, temos:

x 2 +   y 2 = 36 - 12 y + y 2 9

9 x 2 +   9 y 2 = 36 - 12 y + y 2

9 x 2 + 8 y 2 + 12 y = 36

Para chegar na equação final da cônica, vamos completar quadrados!

9 x 2 + 8 y + 3 2 y = 36

9 x 2 + 8 y + 3 4 2 = 36 + 9 2

9 x 2 + 8 y + 3 4 2 = 81 2

Dividindo a expressão toda por 81 2 , temos

x 2 9 2 + y + 3 4 2 81 16 = 1  

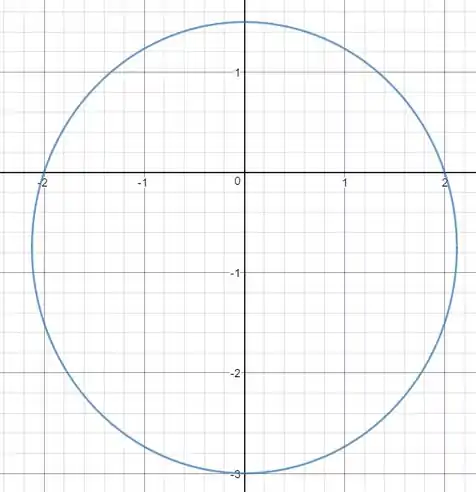
Essa é a expressão de uma elipse!! Seu esboço será:

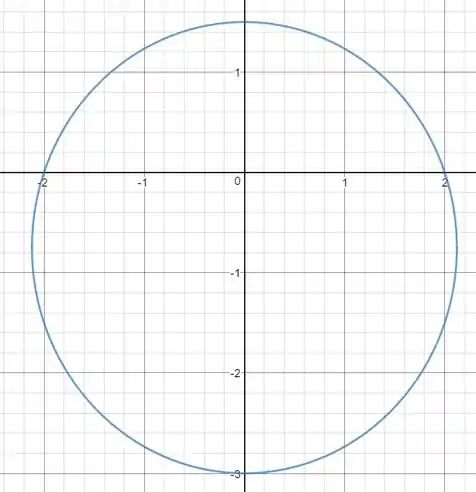
Resposta

x 2 9 2 + y + 3 4 2 81 16 = 1

Essa é a expressão de uma elipse!!

Exercício Resolvido #5

Lista Unicamp – Geometria Analítica. Questão 488

Encontre uma equação em coordenadas polares para a curva cuja equação em coordenadas cartesianas é dada por 2 x y = 25 .

Passo 1

Vamos relembrar as relações entre o sistema cartesiano e o polar:

x = r . cos ⁡ θ         ( 1 )

y = r . sin ⁡ θ         ( 2 )

x 2 +   y 2 = r 2 → r = x 2 +   y 2       ( 3 )

Belezinha! Agora vamos substituir ( 1 ) e ( 2 ) na equação do enunciado:

2 r c o s θ r s i n θ = 25

2 r 2 c o s θ s i n θ = 25

r = 25 2 c o s θ s i n θ

Lembrando que 2 c o s θ s i n θ = s i n ⁡ ( 2 θ )

r = 5 sin ⁡ 2 θ

Uhullll

Resposta

r = 5 sin ⁡ 2 θ

Exercício Resolvido #6

Unicamp, P3 – Geometria Analítica, 01/07/2009, Professor Marcelo M. Santos, pág. 1, Questão 1-item a

Identifique a cônica dada em coordenadas polares, determine a sua equação em coordenadas cartesianas e faça um esboço do seu gráfico:

i )   r = - 3 cos ⁡ θ

i i )   r = 5 2 - 2 cos ⁡ θ

Passo 1

Vamos lá!! O enunciado nos dá três equações em coordenadas polares e a partir delas devemos identificar qual cônica a expressão representa. Além disso, devemos passar a equação para o sistema cartesiano e fazer um esboço do seu gráfico. Bora, começar então?!

Passo 2

                    i )   r = - 3 cos ⁡ θ

Olhando para a expressão fica meio difícil de dizer qual cônica é, certo?!! Então, vamos passar primeiro para o sistema cartesiano já que o jeitão das cônicas nós vimos em coordenadas cartesianas. Para facilitar nossa vida hehe!!

Já que estamos em coordenadas polares e queremos passar para as coordenadas cartesianas, vamos utilizar as seguintes relações que aprendemos na teoria:

x = r . cos ⁡ θ         ( 1 )

y = r . sin ⁡ θ         ( 2 )

x 2 +   y 2 = r 2 → r = x 2 +   y 2       ( 3 )

Substituindo a expressão ( 3 ) na equação dada pelo enunciado, temos:

r = - 3 cos ⁡ θ →   x 2 +   y 2     = - 3 cos ⁡ θ   ( 4 )

Pela expressão ( 1 ) e rearranjando a mesma, temos:

x r = cos ⁡ θ     ( 5 )

Substituindo ( 5 ) na expressão ( 4 ) :

x 2 +   y 2     = - 3 cos ⁡ θ

x 2 +   y 2     = - 3 x r       ( 6 )

Sabendo da expressão ( 3 ) o valor de r em função de x e y , e substituindo na expressão ( 6 ) :

x 2 +   y 2     = - 3 x r   →   x 2 +   y 2     = - 3 x x 2 +   y 2          

x 2 +   y 2 = - 3 x

Chegamos numa expressão cartesiana agora devemos arrumá-la para que ela fique com o jeitão de alguma das cônicas para que então possamos identificar a cônica:

x 2 +   y 2 = - 3 x →   x 2 +   y 2 + 3 x = 0

Completando quadrado temos:

x + 3 2 2 - 9 4 + y 2 = 0

x + 3 2 2 + y 2 = 9 4

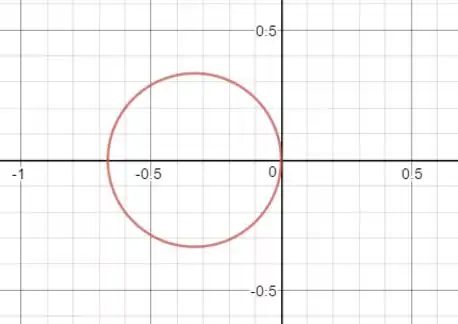
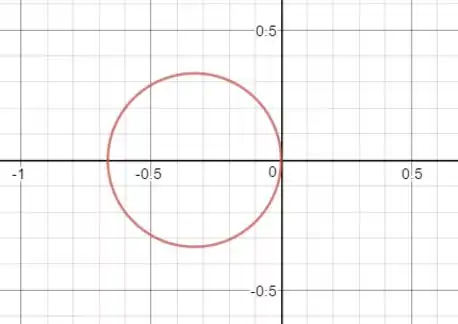
Pela expressão a cônica é um círculo de centro C = - 3 2 , 0 e r = 3 2 . Vimos também, que um círculo nada mais é que uma elipse de excentricidade 0 .

Portanto, fazendo um esboço, temos:

Passo 3

i i )   r = 5 2 - 2 cos ⁡ θ

O passo a passo é o mesmo do item anterior!! Então, vamos achar primeiro a equação em coordenadas cartesianas!!

Substituindo as relações anteriores 1 ,   ( 2 ) e ( 3 ) na equação dada pelo enunciado, teremos:

r = 5 2 - 2 cos ⁡ θ →   x 2 +   y 2   =   5 2 - 2 cos ⁡ θ

Substituindo cos ⁡ θ = x r → cos ⁡ θ = x x 2 +   y 2 , teremos:

x 2 +   y 2   =   5 2 - 2 cos ⁡ θ →   x 2 +   y 2   =   5 2 - 2 x x 2 +   y 2     ( 7 )

Rearranjando a expressão 7 , temos:

x 2 +   y 2   =   5 2 - 2 x x 2 +   y 2

x 2 +   y 2   =   5 x 2 +   y 2 2 x 2 +   y 2 - 2 x

2 ( x 2 +   y 2 ) - 2 x x 2 +   y 2 = 5 x 2 +   y 2

2 ( x 2 +   y 2 ) = ( 5 + 2 x ) x 2 +   y 2

Elevando os dois lados ao quadrado:

4 x 2 +   y 2 2 = ( 5 + 2 x ) 2 ( x 2 +   y 2 )

x 2 +   y 2 4 ( x 2 +   y 2 ) - 5 + 2 x 2 = 0

x 2 +   y 2 - 25 - 20 x + 4 y 2 = 0

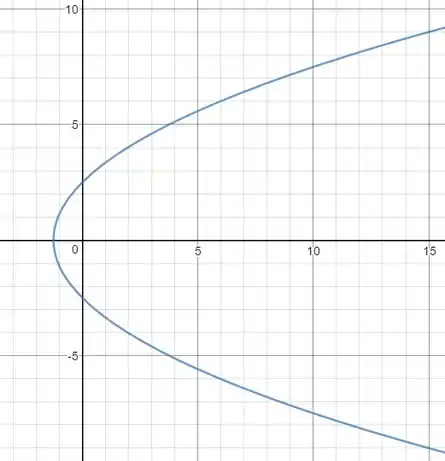
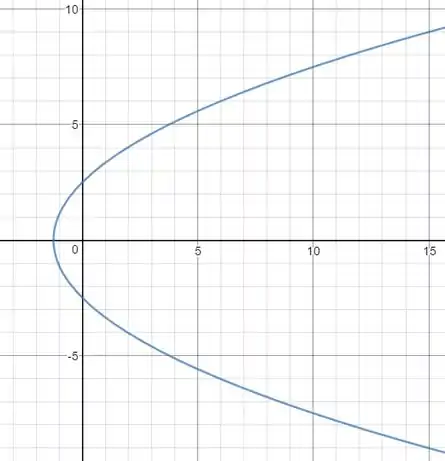
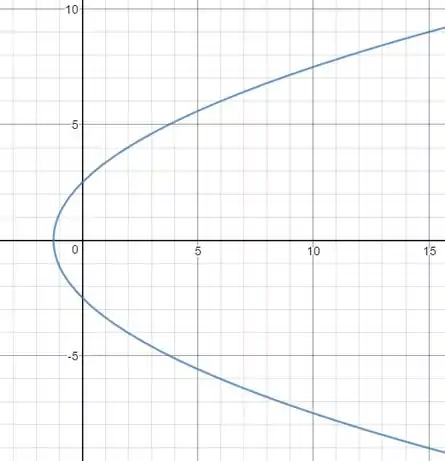
Temos, que x 2 +   y 2 = 0 representa a origem e - 25 - 20 x + 4 y 2 = 0 , essa segunda expressão representa a parábola:

4 y 2 = 25 + 20 x →   y 2 = 25 + 20 x 4

Então, essa expressão representa uma parábola, fazendo o esboço, temos:

Resposta

  1. A cônica é um círculo de centro C = - 3 2 , 0 e r = 3 2 . Vimos também, que um círculo nada mais é que uma elipse de excentricidade 0 .

  2. Uma parábola com equação y 2 = 25 + 20 x 4

Exercício Resolvido #7

Lista Unicamp – Geometria Analítica. Questão 1470

Mostre que, em um sistema de coordenadas polares, a distância d entre os pontos ( r 1 ,   θ 1 ) e ( r 2 ,   θ 2 ) é dada por

d = r 1 2 + r 2 2 - 2 r 1 r 2 c o s ⁡ ( θ 1 - θ 2 )

Passo 1

Eita, enunciado começou com “mostre que” já não gostei!

Calma, galera vocês vão ver que é mais fácil do que parece!

Vamos relembrar de novo as relações entre o sistema cartesiano e o polar:

x = r . cos ⁡ θ         ( 1 )

y = r . sin ⁡ θ         ( 2 )

x 2 +   y 2 = r 2 → r = x 2 +   y 2       ( 3 )

Belezoca! Vamos pensar na distância em coordenadas cartesianas:

d = x 1 - x 2 2 + y 1 - y 2 2

Agora, vamos substituir esses x e y pelas nossas coordenadas polares e vê no que dá!

Passo 2

Substituindo:

d = r 1 c o s θ 1 - r 2 c o s θ 2 2 + r 1 s i n θ 1 - r 2 s i n θ 2 2

d = r 1 2 cos 2 ⁡ θ 1 - 2 r 1 r 2 c o s θ 1 c o s θ 2 + r 2 2 cos 2 ⁡ θ 2 + r 1 2 sin 2 ⁡ θ 1 - 2 r 1 r 2 s i n θ 1 s i n θ 2 + r 2 2 sin 2 ⁡ θ 2

Colocando os termos em comum em evidência

d = r 1 2 ( cos 2 ⁡ θ 1 + sin 2 ⁡ θ 1 ) + r 2 2 ( cos 2 ⁡ θ 2 + sin 2 ⁡ θ 2 ) - 2 r 1 r 2 ( c o s θ 1 c o s θ 2 + s i n θ 1 s i n θ 2 )

Lembrando que:

cos 2 ⁡ θ 1 + sin 2 ⁡ θ 1 = 1

E

c o s θ 1 c o s θ 2 + s i n θ 1 s i n θ 2 = c o s ⁡ ( θ 1 - θ 2 )

Temos que:

d = r 1 2 + r 2 2 - 2 r 1 r 2 c o s ⁡ ( θ 1 - θ 2 )

Resposta

d = r 1 2 + r 2 2 - 2 r 1 r 2 c o s ⁡ ( θ 1 - θ 2 )

Exercícios de Livros Relacionados

Se (x, y) são as coordenadas do ponto P num sistema de eixos ortogonais, quais são as coordenadas polares ( R , θ ) desse ponto?
Identifique o seguinte subconjunto do plano por meio de suas coordenadas polares r , θ : θ = 3 π 4 ,
Descreva o conjunto representado, em coordenadas polares, pela equação R = 3 s i n θ
Num sistema de coordenadas oblíquas em que os semi-eixos positivos formam um ângulo α prove que a rotação do ângulo α em torno da origem leva o segmento O P , onde P = x , y , sobre o segmento O P ' o
Esboce a curva descrita pelo ponto de coordenadas polares R = t eθ = 2 π t quando t assume todos os valores reais positivos.