Transformações Lineares Geométricas
Teoria
Introdução
Já vimos que toda pode ser representada por uma matriz, mas existem algumas matrizes especiais que vale a pena falar aqui!
São matrizes que representam transformações geométricas! Por exemplo, aplicando essa matriz à algum vetor você pode encontrar sua projeção, sua reflexão, ampliá-lo, reduzí-lo ou fazer seu cisalhamento!
Uma coisa interessante sobre essas matrizes que eu citei é que são todas lineares! Fica a dica haha.
Até agora nós vimos apenas matrizes aparentemente “aleatórias” que não faziam nada específico. Elas simplesmente realizavam algumas contas com as componentes dos vetores. Agora vamos ver algumas com um propósito.
Repare que nesse momento veremos apenas projeção e reflexão por eixos e planos coordenados. Mais a frente veremos como realizar essas transformações através de qualquer espaço vetorial. No entanto, é importante que já tenham uma ideia do que se tratam e de qual a ideia por trás delas!
Ampliação e Redução de um vetor
Essa é uma das mais básicas. A dela seria algo do tipo:
Então ela simplesmente pega um vetor e multiplica ele por um escalar, tranquilinho né? Naturalmente, se ela reduzirá o tamanho do vetor, e se ela aumentará o tamanho do vetor.
Perceba que eu restringi o à um número maior que zero. Se , a transformação troca o sentido do vetor.
Se quiséssemos então uma matriz que ampliasse todos os vetores do por um fator . Ou seja, dobrasse eles de tamanho.
Aplicando nos vetores da base canônica:
Jogando esses vetores nas colunas de uma matriz:
De uma forma mais geral, a matriz de ampliação ou redução por um fator no pode ser dada por:
Reflexão de um Vetor
O que acontece se refletirmos um vetor do pelo do eixo ? Essa deve manter inalteradas as componentes do vetor no eixo , enquanto multiplica por as componentes do vetor no eixo .
Por exemplo, :
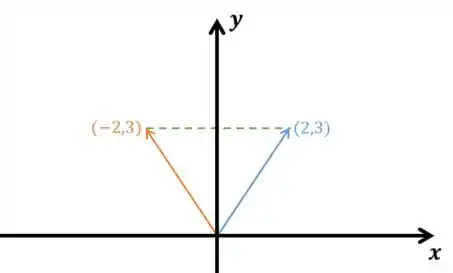
Então, essa deve fazer o seguinte:
Descobrindo a matriz que representa essa :
Tranquilo né? Por enquanto só vamos ver reflexão em torno dos eixos coordenados mesmo, é só pegar a matriz identidade e botar no eixo que vai ser refletido ;)
Um resultado legal das matrizes reflexão é que se você reflete um vetor, depois pega o resultado e reflete ele de novo, ele volta pro vetor inicial! Tipo, se for uma reflexão:
Se pensar geometricamente até que faz sentido né haha.
Projeção de um Vetor
Todos sabem o que significa projetar um vetor, certo? Se quisermos projetar o vetor um vetor do no plano ? Essa matriz deve manter inalterados as componentes do vetor no plano , enquanto zera as componentes do vetor no eixo .
Por exemplo, :
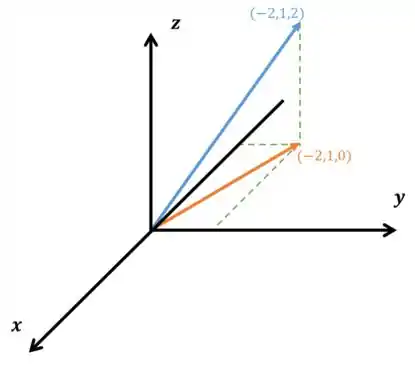
Então, essa faz algo do tipo:
Aplicando na base canônica:
Logo chegamos na matriz:
Cisalhamento
Diferente das transformações aqui em cima, cisalhamento não é um nome tão conhecido haha. Primeiro vamos ver o que ele faz:
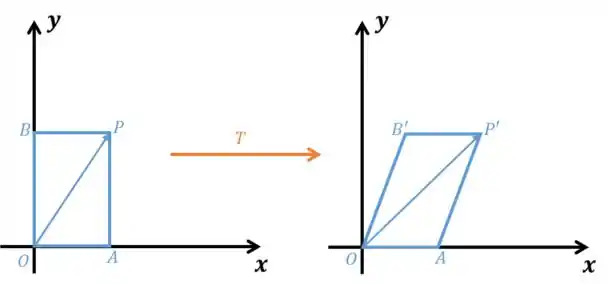
E aí, entendeu? Não né haha. Bom, o que ela faz é transformar o retângulo no paralelogramo , de mesma base e mesma altura.
Nesse caso temos um cisalhamento no eixo , e a transformação seria dada por:
Onde
Perceba que cada ponto se desloca paralelamente ao eixo dos até chegar em , tirando os pontos do próprio eixo dos , que permanecem em sua posição, já que no eixo temos .
A matriz seria dada então por:
Nesse caso, é o fator de cisalhamento.
O cisalhamento ao longo do eixo é análogo e tam sua matriz dada por:
Resumindo
Resumindo o que vimos aqui, temos que:
Ampliação e Redução Multiplica o vetor por um escalar positivo. Se , temos redução, se temos ampliação.
Reflexão Reflete um vetor em torno de um subespaço vetorial. Mantém inalteradas as componentes do vetor no subespaço em questão e multiplica por as componentes perpendiculares a esse subespaço.
Projeção Projeta um vetor sobre um subespaço vetorial. Mantém inalteradas as componentes do vetor no subespaço em questão e zera as componentes perpendiculares a esse subespaço.
Cisalhamento “Tomba” um paralelogramo mantendo sua altura e base inalteradas.
Lembrando que o mais importante aqui é você entender esses conceitos xD
Reflexão de um Vetor
Projeção de um Vetor
Cisalhamento
Resumindo
Exercícios Resolvidos
Exercício Resolvido #1
Elaboração Própria
Determine a matriz que realiza as seguintes transformações no :
Amplia todos os vetores por um fator
Reflete os vetores em torno do eixo .
Projeta os vetores no eixo .
Reflete os vetores em torno da reta
Passo 1
Bom, essa matriz representa a que faz o seguinte:
Aplicando na base canônica do :
Logo,
Passo 2
Ao refletirmos os vetores em torno do eixo , nós estamos mantendo as componentes em inalteradas e multiplicando as componentes em por . Logo:
Temos então que:
Com isso,
Passo 3
Quando projetamos os vetores no eixo , estamos mantendo inalteradas as componentes deles em e zerando as componentes de . Portanto:
Então,
E
Passo 4
Essa é um pouco mais complicada. Ela Mantém inalteradas as componentes do vetor sobre a reta e multiplica por as componentes perpendiculares a ela (sobre a reta ). Olha essa imagem pra te ajudar:
Opa, agora ficou fácil. O que ela faz, no final das contas, é trocas as componentes e dos vetores! Logo:
Então,
Resposta
Exercício Resolvido #2
Elaboração Própria
Determine a matriz que realiza as seguintes transformações no :
Projeta os vetores do espaço no plano
Reflete os vetores do espaço em torno do plano
Reflete os vetores do espaço em torno do eixo
Passo 1
Bom, essa matriz representa a que mantém as componentes do vetor sobre o plano inalteradas e zera as componentes sobre o eixo . Então:
Aplicando na base canônica do :
Logo,
Passo 2
Ao refletirmos os vetores em torno do plano , nós estamos mantendo as componentes em inalteradas e multiplicando as componentes em por . Logo:
Temos então que:
Com isso,
Passo 3
Quando refletimos os vetores em torno do eixo , estamos mantendo inalteradas as componentes deles em e multiplicando por as componentes no plano . Portanto:
Então,
E
Resposta
Exercício Resolvido #3
Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 127 – Fix 4.8
Determine (geometricamente, não faça contas) o núcleo e a imagem de cada uma das abaixo de em :
Projeção ortogonal na reta gerada pelo vetor
Reflexão em torno do plano
Projeção ortogonal no plano
Passo 1
Sabemos que a projeção mantém inalteradas as componentes do vetor no subespaço em questão e zera as componentes perpendiculares a esse subespaço.
Logo, as componentes do vetor sobre a reta gerada pelo vetor permanecem as mesmas. Já as componentes perpendiculares à reta são zeradas.
Dessa forma, o núcleo da será o plano , que é o plano perpendicular à .
Já a imagem será a própria reta gerada pelo vetor ! Como ele projeta os vetores sobre essa reta, essa só será capaz de gerar vetores dessa reta, percebe?
Passo 2
Ao refletirmos um vetor nós mantemos inalteradas as componentes do vetor no subespaço em questão e multiplicamos por as componentes perpendiculares a esse subespaço.
Sendo assim, as componentes do vetor sobre o plano permanecerão inalteradas enquanto as componentes do eixo serão multiplicadas por .
Como você pode ver, a reflexão não leva nenhum vetor em especial para o . Então como podemos ver, o núcleo é apenas o . Disso, tiramos que a imagem é todo o .
Passo 3
A reflexão não leva nenhum vetor para o . A projeção, por outro lado, leva! A projeção no plano , mantém as componentes nesse plano inalteradas e leva as componentes perpendiculares à esse plano (eixo ) no .
Logo, o núcleo é o eixo , ou ainda a reta gerada pelo vetor . Já a imagem é o plano .
Resposta
Núcleo é o plano perpendicular a , isto é, o plano . Imagem é a reta gerada por .
Núcleo é o somente. Imagem é todo .
Núcleo é a reta gerada por (o eixo ). Imagem é o plano , gerado pelos eixos e .
Exercício Resolvido #4
Elaboração Própria
O vetor experimenta um cisalhamento horizontal de fator 2. Dê a matriz dessa transformação e o vetor resultante.
Passo 1
Bom a transformação do cisalhamento horizontal é representada pela seguinte expressão:
Substituindo o fator dado:
Temos então a expressão analítica da transformação para um caso geral e podemos achar a matriz facilmente:
Passo 2
Agora vamos achar o vetor resultante da transformação, podemos tanto aplicar na matriz quanto na expressão.
Vou aplicar na expressão:
Resposta
;