Matriz Rotação

Teoria

Uma matriz de rotação, como o próprio nome já diz, é uma matriz que roda um vetor no espaço em que está contido. Vamos nos limitar, no entanto, à rodar um vetor de um ângulo no ou rodá-lo e torno de um eixo no .

Rotação no

Temos então uma transformação , tal que . Onde é o vetor rotacionado de graus.

Para descobrirmos a matriz que faz isso, precisamos primeiro descobrir qual a equação de . Para isso precisamos saber e . Vamos começar visualizando o que acontece quando rodamos esses vetores:

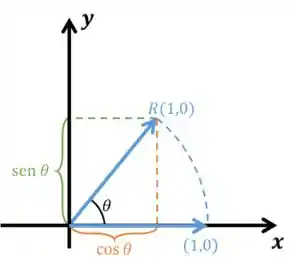
Com essas imagens fica fácil né! Temos que:

Logo,

Obs: Lembrando que essa é a matriz que representa a rotação no sentido trigonométrico (anti-horário)! A matriz rotação no sentido horário ficaria assim (resolve aí):

Rotação no

Vamos agora para a rotação no !

Note que agora temos que especificar o eixo de rotação. Então, como você já deve ter imaginado, teremos matrizes possíveis, já que temos sentidos possíveis de rotação em torno de eixos! Vamos ver um exemplo:

Temos , tal que . Onde é o vetor rotacionado de graus em torno do eixo .

Para encontrarmos a matriz que representa precisamos descobrir quanto vale , e . Bom, como a rotação é em torno de , os vetores que estão no eixo permanecem inalterados:

Já para os vetores e , teremos:

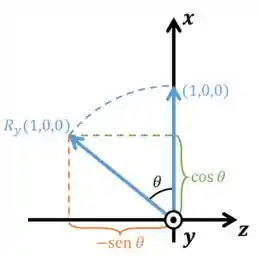
Logo, teremos:

Portanto,

Se quiséssemos rodar para o outro lado:

Analogamente, podemos achar a matriz de rotação em torno do eixo :

E em torno do eixo :

É claro que não vamos gravar todas essas matrizes né! Se olharmos com atenção podemos ver um padrão nas rotações do . Fora que elas são construídas usando a matriz rotação do ! Então, gravando a do , praticamente já temos as do prontas.

Você pode também deduzir na hora a matriz como fizemos aqui haha xD

Rotação fora da Origem

Bom, até aqui vimos como girar vetores em tornos dos eixos coordenados certo? Bom e se quisermos girá-los em torno de um eixo deslocado?

Po como assim? Vou te dar um exemplo prático pra ficar melhor de entender:

Os pontos , e são vértices de um triângulo equilátero. Determinar o vértice , utilizando a matriz rotação.

Sabemos que um triângulo equilátero possui os lados iguais e os ângulos de . Então, temos duas opções para continuar o problema:

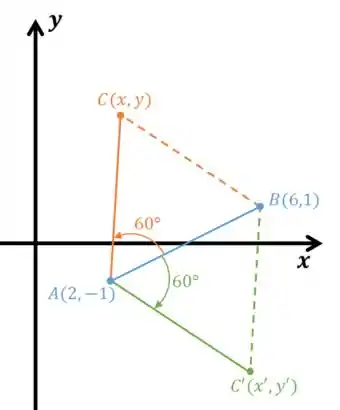
Podemos rodar em torno de no sentido horário ou no sentido anti-horário. Vamos usar o sentido trigonométrico e girar o vetor no sentido anti-horário.

Bom, temos um problema então, pois não sabemos fazer isso! Bom, vamos aprender né. Se liga, que é mais fácil do que aparenta. Temos que:

E sabemos que:

Agora resolvemos o sistema:

Dessa igualdade, chegamos ao sistema:

Logo,

O ponto então é :

Rotação no R 3

Rotação fora da Origem

Exercícios Resolvidos

Exercício Resolvido #1

Marco Cabral e Paulo Goldfeld, Curso de Álgebra Linear Fundamentos e Aplicações, 3ª Ed., Rio de Janeiro, Instituto de Matemática, 2012, pp. 126 – Fix 4.4

Qual das alternativas apresenta a matriz que roda os vetores do por um ângulo (no sentido trigonométrico, isto é, anti-horário):

Passo 1

Como vimos na teoria, temos:

Portanto,

Logo,

Resposta

Letra

Exercício Resolvido #2

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 222. – 46

Os pontos e são vértices consecutivos de um quadrado. Calcular os outros dois vértices, utilizando a matriz rotação.

Passo 1

Antes de começarmos, é bom frizar que não é necessário nenhum conhecimento especial pra fazer esse problema haha. Vou botar as imagens pra vocês verem o que tá acontecendo mas não seria necessário!

Bom, temos o seguinte:

Para acharmos outro vértice através da rotação podemos girar em torno de de ! Então, temos que:

Onde,

Obs: Cuidado com o sinal dos senos! Nesse caso estamos girando no sentido horário, então o sinal fica no seno de baixo.

Chegamos na equação:

Temos então:

O que implica que:

Encontramos o ponto

Passo 2

Agora vamos achar o vértice do quadrado! Para isso, vamos girar em torno de no sentido anti-horário:

Onde,

Resolvendo a equação:

Dessa forma,

Logo,

Portanto, temos

Passo 3

E está pronto nosso quadrado ;)

Alternativamente, poderíamos rodado para o outro lado, de forma que encontraríamos o quadrado:

Resposta

e ou e

Exercício Resolvido #3

Alfredo Steinbruch e Paulo Winterle, Álgebra Linear, 2ª ed., São Paulo, Pearson, 1987, pp. 222. – 47

Os pontos , e são vértices de um triângulo retângulo isósceles, reto em . Determinar o vértico fazendo uso da matriz rotação.

Passo 1

Beleza, temos esses pontos:

Bom, sabemos que o ângulo em vale e que o triângulo é isósceles! Isso quer dizer que os lados e são iguais! Então, basta girarmos em torno de de um ângulo de :