Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 1.8 - Ex. 17
17. (a) Encontre uma equação que represente a família de todos os polinômios de grau dois que passam pelos pontos (0,1) e (1,2)
(b) Esboce quatro curvas da família obtida a mão ou co a ajuda de uma ferramenta gráfica.
Passo 1
Precisamos de três pontos para obtermos um polinômio de grau dois, então vamos definir um ponto arbitrário:
Com esses três ponto teremos essas três equações:
Do ponto :
Do ponto :
Como
Do ponto :
Como
O sistema formado por essas equações é o seguinte:
Escrevendo na forma matricial:
E escrevendo a matriz estendida:
Passo 2
Vamos escalonar a matriz para encontrar a solução do sistema.
Somando vez a primeira equação na segunda:
Dividindo a segunda equação por :
Somando vez a segunda equação na primeira:
Ou seja, a solução do sistema é:
A equação fica:
Passo 3
(b)
Vamos pegar 4 valores para o ponto e desenhar o gráfico que obtemos da equação:
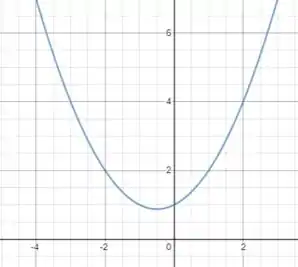
Para :
Fazendo o desenho desse gráfico vamos obter:
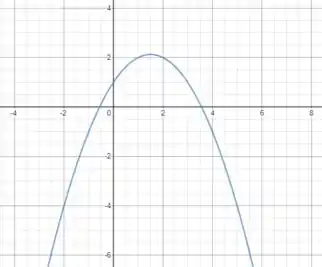
Para :
Essa é a mesma equação que encontramos anteriormente. Ou seja o gráfico é igual:
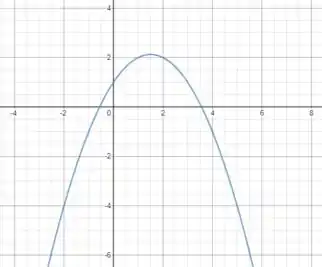
Para :
Fazendo o desenho desse gráfico vamos obter:
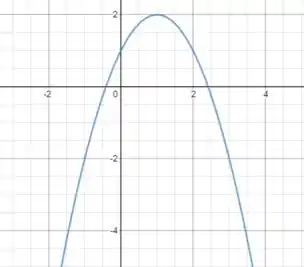
Para :
Fazendo o desenho desse gráfico vamos obter:
