Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 1.Exercícios Propostos - Ex. 11
É dado um triângulo ABC e o ponto X sobre a reta AB tal que . Sejam e
- Determine o vetor em função de e .
- Seja M o ponto médio de . Escreva em função de e .
Passo 1
Fala, galera! Prontos para resolver mais uma questão? Essa questão parece complicada, mas tem um pulo do gato. O enunciado diz que o ponto X é posicionado sobre a reta AB de tal forma que . Isso quer dizer que os dois vetores estão na mesma direção e sentido. Vamos começar desenhando um triângulo genérico para facilitar a visualização:
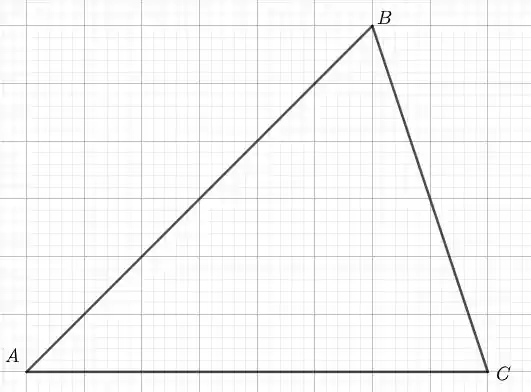
Se o ponto X estivesse entre A e B, teríamos na verdade algo como . Percebeu a diferença? Não? Não tem problema. Como o vetor sai de X e vai até B, o vetor sai de X e vai até A e os dois têm o mesmo sentido, então o ponto X não pode estar dentro do triângulo. Veja só a figura abaixo:
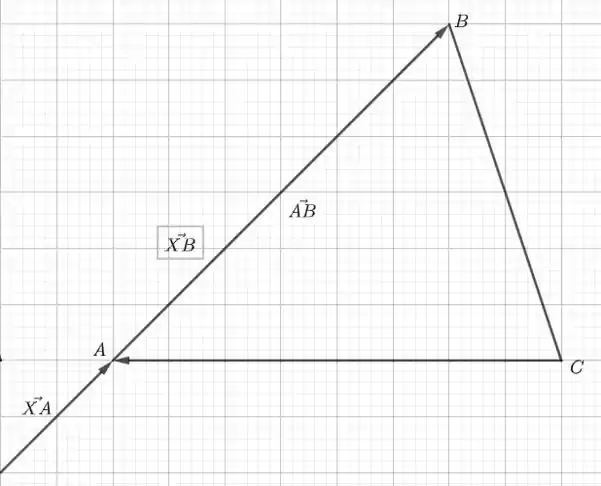
Ficou claro agora? Ótimo! Vamos continuar. A partir da figura acima, vemos que o vetor é a soma dos vetores e , ou seja
Passo 2
- Calma que o passo anterior foi só um aquecimento. Agora vamos realmente começar a resolver a questão. Na figura seguinte, podemos ver que é possível ir de C a X diretamente (o que corresponde ao vetor ) ou ir de C a A (o que corresponde ao vetor ) e depois de A a X (o que corresponde ao vetor ). Então, isso quer dizer que
- O ponto M é o ponto médio de , então desenhamos o vetor na figura do triângulo. Você provavelmente deve lembrar do Exercício Resolvido 3 a propriedade de que . Agora, só precisamos escrever e em termos de e . No passo 1, vimos que . Então,
Passo 3
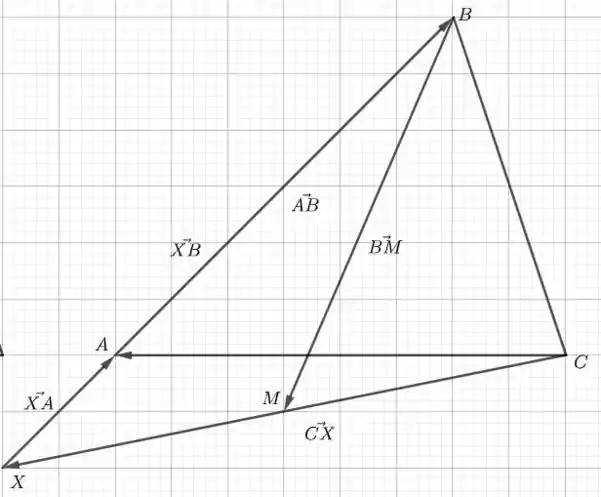
A partir da figura, conseguimos identificar que
Assim, usando os resultados dos passos anteriores, obtemos