Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 15.Problemas - Ex. 3
Prove que a soma dos vetores com origem no centro de um polígono regular e extremidade nos vértices desse polígono é igual a zero.
Passo 1
Fala aiii meus lindos tudo blz? espero que sim
Nessa questão ele pede para provar que a soma dos vetores com origem no centro de um polígono regular e extremidade nos vértices desse polígono é igual a zero.
Precisa fazer esta carinha não que ela parece difícil mais é de boa.
Passo 2
sabendo que,
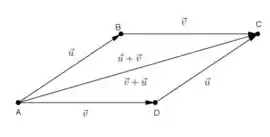
Tendo,
Ficando;
Espero que eu tenha ajudado e te vejo no próximo desafio.
Até a próxima.
Resposta
Exercícios de Livros Relacionados
Mostre que qualquer conjunto com mais de três vetores em P 2 é linearmente dependente.
Mostre que se S={ v 1 ,v 2 ,v 3 } for um conjunto linearmente dependente de vetores num espaço vetorial V e se v 4 for um vetor qualquer em V que não está em S , então { v 1 ,v 2 ,v 3 ,v 4 } também é
Mostre que se S={ v 1 ,v 2 ,...,v r } for um conjunto linearmente dependente de vetores num espaço vetorial V e se v r + 1 ,...,v n forem vetores quaisquer em V que não estão em S , então { v 1 ,v 2 ,
Prove: dados quaisquer vetores u ,v e w num espaço vetorial V , os vetores u -v , v -w e w -u formam um conjunto linearmente dependente.
Prove: o espaço gerado por dois vetores em R 3 é uma reta pela origem, um plano pela origem, ou a própria origem.