Enunciado
Cálculo - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 5.2 - Ex. 6
6. Achar uma função que esteja no núcleo do operador , cujo valor para seja e tal que o valor de sua derivada em seja 1. Fazer o gráfico dessa função.
Passo 1
- pra uma função estar no núcleo do operador, devemos ter:
Passo 2
Vamos agora pensar numa função que satisfaça as condições que ele disse no enunciado:
Hmmmm... e se a gente integrar a derivada? (calma que é beeem simpleszinho)
Onde é a constante de integração.
Perfeito... e agora:
Então a função vai ser:
Passo 3
Vamos ver agora se ela está no núcleo do operador, ne... (e rezar para que sim, senão vamos precisar achar outra)
Amém
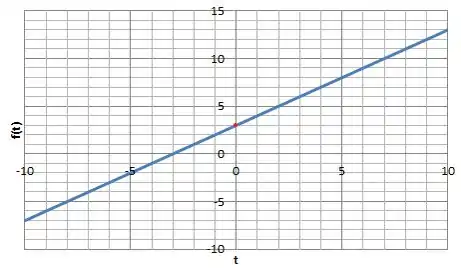
Passo 4
Agora só falta o gráfico, que pra nossa alegria é uma reta , né..... E sabemos que ela corta o eixo em 3, pois ...
Resposta
Exercícios de Livros Relacionados
Ache a solução completa para a equação diferencial: d y d x = 1 - 2 x y 1 + x 2
Ache a solução da equação diferencial que satisfaça a condição dada. x 2 + 1 d y d x + 2 x y = x 2 ; y = 0q u a n d ox = - 1
Ache a solução da equação diferencial que satisfaça a condição dada. d y d x - y x = y - x ; y = 2q u a n d ox = 1
Ache uma solução da equação diferencial que satisfaça a condição dada. x d y d x = 2 y + 4 x 2 ln x ; y = 4 quando x = 1 .
Ache uma solução da equação diferencial que satisfaça a condição dada. d y d x = 1 + 2 y cotg x ; y = 2 quando x = 1 4 π .