Enunciado
Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 1.1 - Ex. 1c
Achar os valores e os vetores próprios do operador do dado por:
c.
Passo 1
Primeiro, vamos colocar em forma de matriz de e que seria, para isso vamos colocar em um sistema para ficar claro
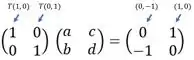
Assim teremos o sistema
Substituindo, encontramos a matriz!
Vamos usar a formulazinha para descobrir os valores próprios
Lembrando que é a matriz identidade e o é o valor que queremos descobrir, logo
Passo 2
Vamos subtrair
Certinho? Então descobrimos , agora falta colocar no determinante!
Então calculando o determinante temos a equação característica
Uhuul! Encontramos o polinômio característico!
Mas como não existe raiz quadrada negativa dentro dos reais, concluímos que não existe solução de autovalores e vetores para os reais.
Resposta
Não existem valores e vetores próprios reais
Exercícios de Livros Relacionados
Calcular o polinômio característico e os valores próprios da matriz: 2 1 0 0 0 2 0 0 0 0 1 1 0 0 - 2 4
Provar que se λ é valor próprio de T, então λ n é valor próprio de T n . Generalizando, se p(t) é um polinômio então p ( λ ) é valor próprio de p(T), onde p T =a 0 1+ a 1 T+ . . .+a n T n se p ( t )=a
Sejam A e B matrizes triangulares com a mesma diagonal principal ( a i i=b j j ,i =1 ,. . . ,n ) . Prove que: P A ( t )=P B ( t )
Determinar valores próprios do operador linear T : V → V do R 4 que é definido em uma base { e 1 ,..., e n } por T e i = λ i ∈ R .
Seja A uma matriz triangular, ou seja, uma matriz A=( a i j ) tal que a i j = 0 sempre que ij (ou, ao contrário, a i j = 0 , sempre que i