Enunciado
Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 7.Exercícios Propostos - Ex. 31
Ache equações paramétricas da reta , simétrica da reta em relação ao plano .
Passo 1
Galerinha, nessa questão temos que seguir o seguinte roteiro:
- Escrever as equações paramétricas da reta .
- Encontrar o vetor diretor da reta e determinar se a reta é concorrente ao plano. Se sim, encontrar o ponto de interseção.
- Encontrar o vetor diretor da nova reta.
Passo 2
Então, vamos começar com os dois primeiros pontos do roteiro. A equação paramétrica da reta são
Com isso, é fácil identificar que o ponto pertence a reta e que o vetor diretor da reta é . Além do mais, o vetor normal do plano é dado por . Então, o produto interno dos dois vetores é
Com isso, vemos que a reta é concorrente ao plano. Agora, vamos substituir as equações paramétricas da reta na equação do plano e tentar determinar para que valor a reta cruza o plano:
O ponto é dado por . Esse ponto pertence tanto à reta quanto ao plano. Um detalhe muito importante é que a reta cruza o plano exatamente nesse ponto. Então, temos
Passo 3
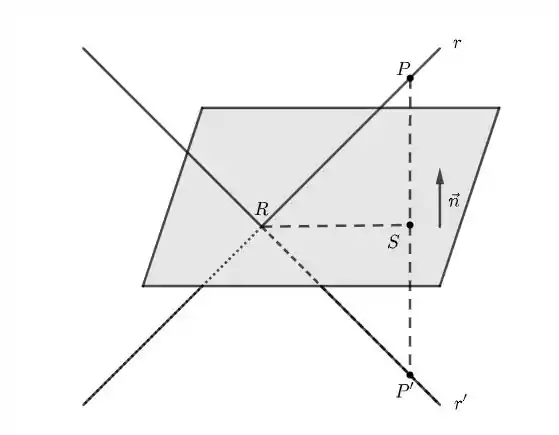
O vetor normal do plano cruza o vetor diretor da reta em algum momento. Vamos dizer que isso ocorre quando , ou seja, no ponto . Com isso, podemos escrever o vetor normal ao plano da seguinte forma parametrizada:
onde corresponde ao ponto . Ou seja, e se cruzam no ponto . Ok, agora vamos procurar o ponto onde cruza o plano
Se em , o vetor normal é concorrente a e ele é concorrente ao plano. Isso corresponde ao ponto
do plano. Do ponto de interseção da reta com o plano até o ponto de interseção do vetor normal com o plano, temos
Por outro lado, de até , temos
Assim, o vetor diretor da segunda reta será paralelo a
Nós podemos escolher o fator de proporcionalidade em . Para simplificar o resultado, vamos escolher . Assim, ficamos com e a equação paramétrica de será: