Enunciado
Álgebra Linear e Geometria Analítica - Álgebra Linear - 3ª Edição - J. L. Boldrini- Ed: 3º - Capítulo 7.5 - Ex. 15
Considere o sistema mecânico mostrado na figura abaixo
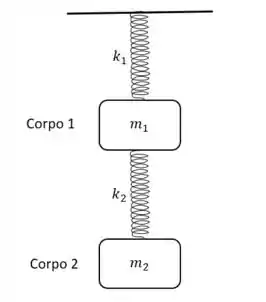
Utilizando os procedimentos da secção 7.1.5 estude a vibração do sistema quando ele é tirado da posição de equilíbrio. Resolva completamente descrevendo o comportamento do sistema no caso em que , , , . Os deslocamentos iniciais dos corpos 1 e 2 são, respectivamente, para cima e para baixo.
Passo 1
O problema não falou nada sobre gravidade, então não vamos nos importar com o peso dos blocos.
O primeiro passo é escrever a equação do movimento desses blocos. Seja e o deslocamento desses corpos em relação à posição de equilíbrio em um dado instante ambos para baixo. Da física podemos escrever:
Depois organizamos as equações para que fiquem no formato requerido pela secção 7.1.5:
Podemos reescrever o sistema como:
Passo 2
Vamos calcular as entradas da matriz dos coeficientes:
E a matriz fica:
Passo 3
Devemos diagonalizar a matriz. Realizando a diagonalização, temos:
Utilizando os resultados da seção 7.1.5, temos:
Onde e estão na base dos autovetores.
Passo 4
Esse sistema gera as equações:
Como e são ambos negativos, as soluções dessas EDO’s são:
Seja a matriz de mudança de base da base dos autovetores para a canônica, temos que:
Logo:
Passo 5
Para encontrar as constantes basta usarmos as condições de contorno:
- e ;
- e .
Substituindo nas equações encontradas acima chega-se à resposta.
Resposta
Demonstração.