Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.5 - Ex. 10

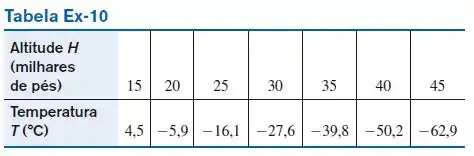
A Agência Espacial dos Estados Unidos utilizou uma espaçonave experimental leve pilotada remotamente e movida a energia solar, denominada Pathfinder, numa série de experimentos para determinar a viabilidade da utilização de energia solar em voos de grande altitude e longa duração. Em agosto de 1997 , a Pathfinder registrou os dados da tabela dada que relacionam a altitude H com a temperatura T . Mostre que é razoável um modelo linear esboçando os pontos de dados e encontre o ajuste linear de mínimos quadrados H = H 0 + k T .

Passo 1

Oi pessoal, tudo bem? Vamos analisar essa questão.

Vamos plotar os pontos fornecidos, depois faremos um ajuste linear com estes pontos e plotaremos a função correspondente para compararmos o modelo linear esboçando os pontos com o ajuste linear de mínimos quadrados.

Temos então que:

M = 1 1 1 1 1 1 1       1 5 2 0 25 30 35 40 45

Temos que:

M T M = 1 15       1 20       1 25       1 30       1 35       1 40       1 45 1 1 1 1 1 1 1       15 20 25 30 35 40 45

M T M = 7 210       210 7000

Passo 2

A inversa será:

M T M - 1 = 1 4900 7 000 - 210       - 210 7

Agora vamos aplicar o ajuste linear. Temos que:

V * = M T M - 1 M T y

Substituindo, teremos:

V * = 1 4900 7000 - 210       - 210 7 - 198 - 7512,5

Resolvendo, temos que:

V * = 39,11 - 2,25

Portanto nosso ajuste linear será:

H = 39,11 - 2,25 T

Passo 3

Plotando a reta e os pontos temos que:

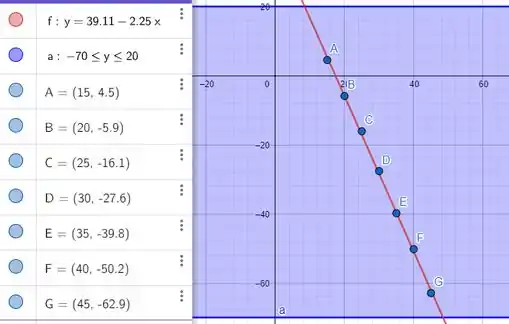
É nítido que um modelo linear esboçando os pontos de dados é razoável e pode ser comparado a um ajuste linear.

Resposta

Ei, a resposta está no passo a passo :)

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Encontre a curva da forma y = a + ( b / x ) que melhor ajuste os pontos ( 1 ,7 )( 3 ,3 )e( 6 ,1 ) fazendo a substituição X = 1 / x . Esboce a curva e marque os pontos de dados no mesmo sistema de coor
Existe algum valor de s com o qual x 1 = 1 e x 2 = 2 seja a solução de mínimos quadrados do sistema linear dado?x 1 - x 2 = 1 2 x 1 + 3 x 2 = 1 4 x 1 + 5 x 2 = s Explique seu raciocínio.
Prove: se A tiver vetores coluna linearmente independentes e b for ortogonal ao espaço coluna de A , então a solução de mínimos quadrados de A x = b é x = 0 .
4. Em cada parte, encontre a solução de mínimos quadrados do sistema linear A x = b → .(a) A = 3 2 - 1 1 - 4 3 1 10 - 7 ;b → = 2 - 2 1 (b) A = 2 0 - 1 1 - 2 0 2 - 1 0 0 1 - 1 ; b → = 0 6 0 6
6. Em cada parte, encontre o vetor erro e → = b → - A x → que resulta da solução de mínimos quadrados x → e verifique que é ortogonal ao espaço coluna de A .(a) A e b → como no Exercício 4(a)(b) A e b