Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 6.5 - Ex. 11
Encontre a curva da forma que melhor ajuste os pontos fazendo a substituição . Esboce a curva e marque os pontos de dados no mesmo sistema de coordenadas.
Passo 1
Oi pessoal, tudo bem? Vamos analisar essa questão.
Temos que:
E:
Vamos encontrar o termo :
Passo 2
A inversa será:
Agora vamos aplicar o ajuste linear. Temos que:
Substituindo, teremos:
Resolvendo, temos que:
Portanto nosso ajuste linear será:
Substituindo por , obtemos a curva necessária:
Passo 3
O gráfico da curva é dado por:
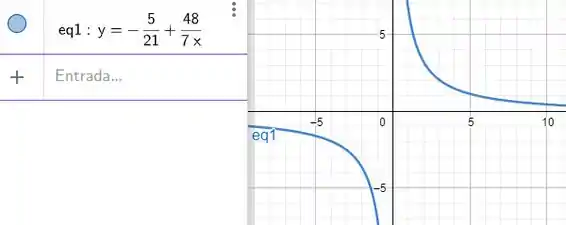
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
1. Sejam u = 1,2 , - 1 , v = 3,1 , 0 e w = 0,0 , 2 em R 3 . Calcular:a) u , u ; b) u , w ; c) u , v + w ; d) u , u ; e) u + v 2 ; f) u - v 2 .
9. Pelos exercícios 7 e 8 a função u↦ p r o j g u é uma transformação linear de R n em R n . Quais são seu núcleo o e sua imagem?
1. Sejam u = 1,2 , - 1 , v = 3,1 , 0 e w = 0,0 , 2 em R 3 . Calcular:a) u , u ; b) u , w ; c) u , v + w ; d) u , u ; e) u + v 2 ; f) u - v 2 .
1. Sejam u = 1,2 , - 1 , v = 3,1 , 0 e w = 0,0 , 2 em R 3 . Calcular:a) u , u ; b) u , w ; c) u , v + w ; d) u , u ; e) u + v 2 ; f) u - v 2 .
4. Calcular p r o j gu nos seguintes casos: u = 1,2 , 1,4 e g = 4,0 , 0,1 ; u = 1,1 , 1,1 e g = 2,2 , 2,2 ; u = 4,3 , 5,2 , 5 e g = 1,1 , 1,1 , 1 .