Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 8.Problemas - Ex. 4
Que ângulos faz a reta com os eixos e ?
Passo 1
Faaala, galeeeera!
Abaixo temos a representação da reta e os ângulos que devemos obter. Primeiramente, precisamos encontrar o ponto em que a reta corta o eixo .
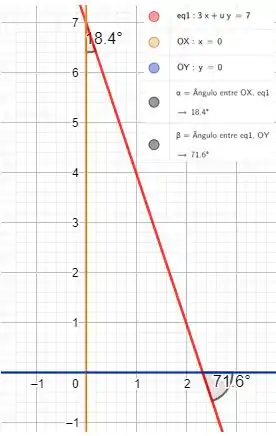
Quando , encontramos o ponto em que a reta corta o eixo . Temos então:
Assim, o valor é aproximadamente .
Temos então que o comprimento do eixo é , ou seja, é o valor em que a reta corta o eixo . Esse valor é sempre a constante (que não está multiplicando uma variável).
O comprimento do eixo é .
O ângulo será então:
O ângulo será então:
Prontinho!
Resposta
Exercícios de Livros Relacionados
O ângulo A ^ do triângulo isósceles A B C mede 120 ° . Sabendo que A = 1,1 , 1 e que B C está contida na reta r : X = 2,1 , 0 + λ 1 , - 1,0 , determine B e C e o comprimento da altura relativa ao vért
Seja θ = a n g ( r ,s ) . Calcule s e nθ nos casos (a) e (b) e cos θ nos casos (c) e (d):c) r : x + 3 z = 7 y = 0 s : x - 4 y - 2 z = 5 y = 0
Seja θ = a n g ( r ,s ) . Calcule s e nθ nos casos (a) e (b) e cos θ nos casos (c) e (d):d) r : x = 1 - y 2 = z 3 s : 3 x + y - 5 z = 0 x - 2 y + 3 z + 1 = 0
Seja θ = a n g ( r ,s ) . Calcule s e nθ nos casos (a) e (b) e cos θ nos casos (c) e (d):b) r : X = 3 ,- 2 ,0 + λ 1 ,- 1 ,2 s : X = - 2 ,3 ,- 5 + λ 1 ,1 ,2
Seja θ = a n g ( r ,s ) . Calcule s e nθ nos casos (a) e (b) e cos θ nos casos (c) e (d):a) r : X = - 5 2 ,2 ,0 + λ 1 2 ,1 ,1 s : z = 3 x = 2 y - 16