Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento geométrico - Ex. 5a
Apresentar, graficamente, um representante do vetor nos casos:
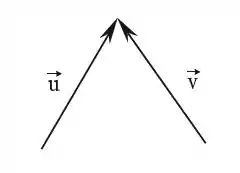
Passo 1
Vamos lá, vamos primeiro mudar o vetor, temos que o vetor tem mesmo módulo e direção, porém sentido contrário de :
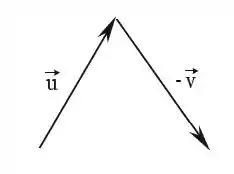
Passo 2
Agora para calcular a soma devemos colocar o ponto de término do vetor tocando o ponto de início do vetor , e como aqui isso já acontece então a soma desses dois vetores é o resultado o ponto de início do primeiro vetor, , com o ponto de término do segundo vetor, :
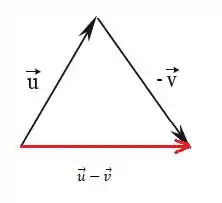
Pronto, temos a representação gráfica do vetor .
Resposta
Ei, a resposta está no passo a passo :)
Exercícios de Livros Relacionados
A interseção X ∩ Y de dois conjuntos convexos X e Y é um conjunto convexo.
Seja X convexo. Se x , y , z ∈ Xeα , β , y são números ≥ 0 com α + β + γ = 1 então α x + β y + γ z ∈ X .
Se α A + β B = C eα A 1 + β B 1 = C 1 , com α + β = 1 , prove que se tem α . A A 1 → + β . B B 1 → = C C 1 → .
Seja 0 ≤ t ≤ 1 . Sabemos que C = A + t . A B → ↔ A C → = t . A B → ↔ C ∈ A B . mostre que, neste caso, tem-se O C → = O A → + t . A B → = 1 - t O A → + t . O B → qualquer que seja o ponto O do plano.
Dados quatro pontos quaisquer A , B , CeD no plano, ponha u = A B → , v = B C → , w = C D → , portanto u + v = A C ,v + w = B D →eu + v + w = A D → . Conclua então que A B → , C D → + A C → , D B → +