Enunciado
Álgebra Linear e Geometria Analítica - Callioli - Álgebra Linear e Aplicações - Parte 2- Ed: 6º - Capítulo 3.2 - Ex. 4
Passo 1
Oi, tudo bem? Bora resolver mais um exercício?
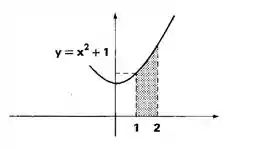
Este exercício nos pede para calcular a área indicada no desenho utilizando os polinômios de Lagrange (veja o exercício - b). E depois, repetir o exercício, tomando o polinômio . Certo?
Se não se lembra desse conteúdo, é hora de dar aquela revisão. Ok?
Passo 2
Vamos lá! De , temos:
E pelo enunciado, (olhando o desenho). Assim, por definição, a área entre e é dada por:
Passo 3
Vamos lá! Agora, para o caso temos que e
Daí,
Resposta
Assim,
Exercícios de Livros Relacionados
Suponha que X 1 , X 2 , … , X n seja um conjunto de vetores do R n linearmente independente. Mostre que se A é uma matriz nxn não singular, então A X 1 , A X 2 , … , A X n também é um conjunto linearm
Mostre que 2 ,t + 1 ,t 2 + 1 , … , t n + 1 , … é um conjunto de polinômios linearmente independente.
Mostre que as funções f 1 t = e λ 1 t ,f 2 t = e λ 2 t , … , f k t = e λ k t , onde λ 1 , … , λ k ∈ R , são linearmente independentes se, e somente se, λ i ≠ λ j , para i ≠ jei , j = 1 , … , k .
Verifique se as funções seguintes são linearmente dependentes ou independentes. a )t , cos t , sin te mC 2 - π , π ; b ) cos t ,1 , sin 2 t 2e mC 2 - π , π ; c )1 ,e t + e - t ,e t - e - t e m
Mostre que as funções f 1 t = t e λ 1 t ,f 2 t = t 2 e λ t , … , f k t = t k e λ k t , onde λ ∈ R , são linearmente independentes.