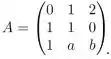Exercícios de CL e DL de Polinômios e Matrizes - Lista de Exercícios Resolvida

Determine se são ou em

(a)

(b)

(c)

Determine para que o conjunto seja

Explique por que os conjuntos de vetores dados são linearmente dependentes.

1. e em
2. e em

Determinar para que o conjunto

Seja

Seja o espaço e os vetores:

Escreva o vetor como combinação linear dos vetores e

Consideramos no espaço os vetores e

1. Escrever o polinômio como combinação linear de .
2. Escrever o vetor como combinação linear de
3. Determinar uma condição para de modo que o polinômio seja combinação linear de
4. É possível escrever como combinação linear de e ?

Quais dos seguintes conjuntos de polinômios pertencentes ao são ?

Verifique que o conjunto abaixo é :

Considere as matrizes:

e

(a) Mostre que a equação pode ser escrita como e use este resultado para resolver em .

38) Seja uma matriz simétrica.

(b) Mostre que é simétrica.

38) Seja uma matriz simétrica.

(a) Mostre que é simétrica.

Considere o polinômio que passa pelos pontos e . Então vale:

a) 28

b) 26

c) 31

d) 25

e) Não sei.

35) Quais das seguintes matrizes são simétricas.

Sejam e considere a matriz:

Se o polinômio característico de for,

então:

(a);

(b)

(c)

(d)

(e)

36) Encontre todos os valores de , e para os quais a matriz é simétrica.