Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 11.Problemas - Ex. 9
Um banco europeu dispõe de 100 milhões de euros para aplicar imediatamente.
Duas opções lhe são oferecidas:
Opção A: 10% ao ano, baixa liquidez.
Opção B: 5% ao ano, alta liquidez.
A diretoria decide que, por segurança, o total investido na opção A no máximo será 3 vezes o que foi investido na opção B. O objetivo do banco é receber o máximo de juros dentro dessas condições. Quantos euros em cada opção deve o banco investir?
Passo 1
Salve galera estudiosa, tudo certin?? É hora da resolução!!! Vamos lá??
Vamos definir as seguintes variáveis para o nosso problema:
X: milhões de euros aplicado na opção A.
Y: milhões de euros aplicado na opção B.
Analisando o contexto do problema temos as seguintes desigualdades:
Além disso, é óbvio que o valor aplicado em cada opção precisa ser maior ou igual a zero, logo:
Representando cada uma dessas desigualdades no plano cartesiano, temos a seguinte região:
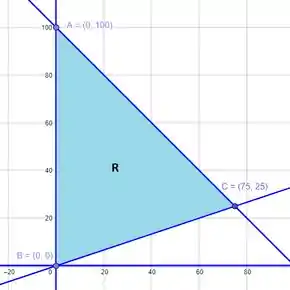
Passo 2
Desejamos agora encontrar nessa região os valores para X e Y que maximizem os juros obtidos, que é dado pela função:
Uma vez que o aumento da opção A é de 10% e da opção B é de 5%.
Um método prático de achar o ponto de máximo da função J consiste em calcular L(P) para todo vértice P da nossa região R e ver qual desses valores é o maior.
Observando melhor a região, conseguimos determinar os vértices A = (0,100), B = (0,0) e C = (75,25) como potenciais candidatos a maximizar o lucro, mas de antemão podemos descartar o ponto B onde nenhum dinheiro foi aplicado.
Calculando os Juros, em A e C, temos que:
Logo, percebemos que a melhor solução é o ponto C, ou seja, para maximizar os juros obtido banco deve aplicar 75 milhões na opção A e 25 milhões na opção B.
Resposta
75 milhões na opção A e 25 milhões na opção B.