Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 3.Problemas propostos - Ex. 18
Mostrar que o quadrilátero de vértices e é um paralelogramo e calcular sua área.
Passo 1
Primeiro, vamos fazer um esboço do nosso quadrilátero :
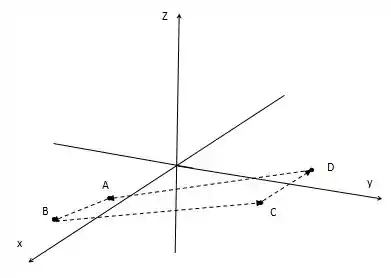
Passo 2
Precisamos mostrar o quadrilátero em questão é um paralelogramo, certo? Mas o que vem a ser um paralelogramo?
Direto ao ponto: um paralelogramo é um quadrilátero (polígono de quatro lados) e seus lados opostos são paralelos. Por consequência, ele tem ângulos opostos e lados opostos congruentes (possuem a mesma forma e o mesmo tamanho).
Dados os pontos e , vamos verificar se os vetores que formam os lados do polígono é um paralelogramo.
Ao encontrarmos os lados, temos:
Lado representado pelo vetor :
E o seu módulo:
Passo 3
Lado representado pelo vetor :
E o seu módulo:
Passo 4
Lado representado pelo vetor :
E o seu módulo:
Passo 5
Lado representado pelo vetor :
E o seu módulo:
Portanto, podemos verificar que e , logo, o polígono é um paralelogramo. 😊
Passo 6
Por fim, para encontrarmos a área, vamos escolher dois vetores NÃO paralelos do polígono e calcular a área utilizando o módulo do produto vetorial entre eles.
Escolhendo os vetores e , temos:
Portanto, a área do paralelogramo é 😉
Resposta
A área do paralelogramo é .