Sabendo que e o ângulo entre e , calcular:
c) a área do paralelogramo determinado por e .
Passo 1
Primeiro, vamos fazer um esboço do nosso problema:
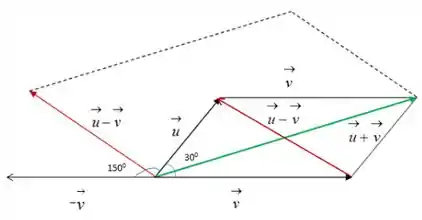
Passo 2
Dado que e é o ângulo entre e :
Como as diagonais formam triângulos, podemos utilizar os conceitos de trigonometria ao utilizar a lei dos cossenos, vamos relembrá-la:
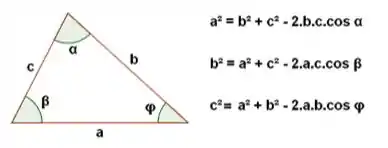
Como característica de um paralelogramo, temos que os ângulos dos vértices opostos do paralelogramo são congruentes:
Para utilizarmos a lei dos cossenos temos que:
Passo 3
Vamos calcular o módulo de e utilizando a lei dos cossenos:
Agora para a soma:
Passo 4
Agora, encontraremos o ângulo formado entre os vetores e , utilizando a fórmula do produto escalar.
Como:
Temos:
Como temos:
Passo 5
O ângulo formando por e é o sen. Assim, temos que:

Portanto, a área do paralelogramo determinado por e é . 😉