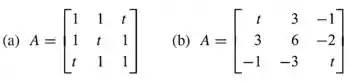
Em cada parte, discuta como o posto de varia com .
Passo 1
Olá! Tudo bem? Vamos resolver esse exercício?!
(b) Primeiro, reduzindo para sua forma escalonada, temos:
Multiplicando por temos:
Multiplicando a primeira linha por e adicionando a segunda linha. Após isso, multiplicando a primeira linha por e adicionando a terceira linha, temos:
Adicionando a segunda linha com a terceira, temos:
Agora, multiplicamos a segunda linha por e adicionamos à terceira:
Portanto, se , o e se , o .
Ainda,
Para possibilitar a resolução, podemos fazer . Então temos:
Logo, se ou , o . De outra forma, o .
Resposta
Veja a resolução completa.