Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.7 - Ex. 5

Em cada parte, encontre a forma vetorial da solução geral do sistema linear A x = b dado e depois use o resultado obtido para encontrar a forma vetorial da solução geral de A x = 0 .

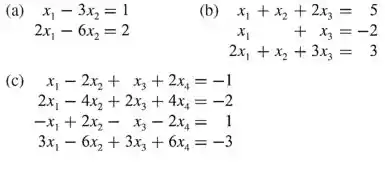
Passo 1

Olá! Tudo bem? Precisamos encontrar a forma vetorial da solução geral do sistema linear A x = b e A x = 0 , em cada item. Então temos:

(a) Primeiro, colocaremos A na forma de matriz e reduziremos A para a sua forma escalonada.

A = 1 - 3 1 2 - 6 2     →     1 - 3 1 0 0 0

Logo, a solução de A x = b é x 1 = 1 + 3 t e x 2 = t ou

x = 1 0 + t 3 1 , na forma vetorial.

Portanto, a solução de A x = 0 é

x = t 3 1

Passo 2

(b) Como fizemos no item (a), agora temos:

A = 1 1 2       5 1 0 1 - 2 2 1 3       3     →     1 0 1 - 2 0 1 1       7 0 0 0       0

Logo, a solução de A x = b é x 1 = - 2 - t , x 2 = 7 - t e x 3 = t ou

x = - 2       7       0 + t - 1 - 1       1 , na forma vetorial.

Portanto, a solução de A x = 0 é

x = t - 1 - 1       1

Passo 3

(c) Novamente, semelhante ao item (a), agora temos:

A =       1 - 2       1       2 - 1       2 - 4       2       4 - 2 - 1       2 - 1 - 2       1       3 - 6       3       6 - 3     →     1 - 2 1 2 - 1 0       0 0 0       0 0       0 0 0       0 0       0 0 0       0

Logo, a solução de A x = b é x 1 = - 1 + 2 r - s - 2 t , x 2 = r , x 3 = s e x 4 = t ou

x = - 1       0       0       0 + r 2 1 0 0 + s - 1       0       1       0 + t - 2       0       0       1 , na forma vetorial.

Portanto, a solução de A x = 0 é

x = r 2 1 0 0 + s - 1       0       1       0 + t - 2       0       0       1

Passo 4

(d) Semelhante aos itens anteriores, agora temos:

A =       1       2 - 3       1       4 - 2       1       2       1 - 1 - 1       3 - 1       2       3       4 - 7       0 - 5 - 5     →     1 0 - 7 / 5 - 1 / 5 6 / 5 0 1 - 4 / 5       3 / 5 7 / 5 0 0       0       0 0 0 0       0       0 0

Logo, a solução de A x = b é x 1 = 6 5 + 7 5 s + 1 5 t , x 2 = 7 5 + 4 5 s - 3 5 t , x 3 = s e x 4 = t ou

x = 6 / 5 7 / 5 0 0 + s 7 / 5 4 / 5 1 0 + t       1 / 5 - 3 / 5       0       1 , na forma vetorial.

Portanto, a solução de A x = 0 é

x = s 7 / 5 4 / 5 1 0 + t       1 / 5 - 3 / 5       0       1

Resposta

Veja a resolução completa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada parte, é dada uma matriz em forma escalonada por linhas. Por inspeção, encontre bases dos espaços linha e coluna de A.(a)1 0 2 0 0 1 0 0 0 (b) 1 - 300 0100 0000 0000 (c)1245 01 - 30 001 - 3 00
Em cada parte, encontre uma base do espaço nulo de A .(a) A = 1 - 13 5 - 4 - 4 7 - 62 (b) A = 2 0 - 1 4 0 - 2 0 00 (c) A =1 4 5 22 1 3 0 - 1 3 2 2 (d) A =145693 - 214 - 1 - 10 - 1 - 2 - 123578 (e) A =
Para as matrizes do Exercício 6 , encontre uma base do espaço linha de A reduzindo a matriz à forma escalonada por linhas.
Para as matrizes do Exercício 6 , encontre uma base do espaço linha de A consistindo totalmente em vetores linha de A .