Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.7 - Ex. 12

Encontre um subconjunto dos vetores dados que forma uma base do espaço gerado pelos vetores; em seguida, expresse cada vetor que não está na base como uma combinação linear dos vetores da base.

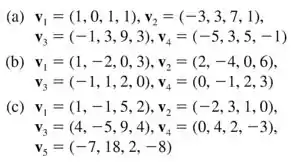
Passo 1

Fala aê!! Blz? Nesta questão podemos proceder da seguinte forma:

Colocaremos os vetores em forma de matriz. Em seguida, escalonaremos e verificaremos quais são os vetores linearmente independentes, os quais formam a base, para, a partir disso, expressarmos os demais vetores como uma combinação linear desses vetores. Veja nos passos a seguir.

Passo 2

(a) Então, de acordo com o que foi dito no passo 1, temos:

A = 1 ⏞ v 1 - 3 ⏞ v 2 - 1 ⏞ v 3 - 5 ⏞ v 4 0       3       3       3 1       7       9       5 1       1       3 - 1   →     Ã = 1 ⏞ v 1 ⏞ i n d e p e n d e t e 0 ⏞ v 2 ⏞ i n d e p e n d e t e 2 ⏞ v 3 - 2 ⏞ v 4 0 1 1       1 0 0 0       0 0 0 0       0

Após o escalonamento, vemos que v 1 e v 2 são linearmente independentes. A partir disto, colocaremos os demais vetores como uma combinação linear desses vetores, veja:

Primeiro, v 3 = a v 1 + b v 2 .

- 1       3       9       3 = a 1 0 1 1 + b - 3       3       7       1   →     a = 2       b = 1 . Logo, v 3 = 2 v 1 + v 2 .

Agora, v 4 = c v 1 + d v 2 .

- 5       3       5 - 1 = c 1 0 1 1 + d - 3       3       7       1   →     c = - 2       d = 1 . Logo, v 4 = - 2 v 1 + v 2 .

Passo 3

(b) Semelhante ao item anterior, temos:

A =       1       2 - 1       0 - 2 - 4       1 - 1       0       0       2       2       3       6       0       3     →     Ã = 1 ⏞ i n d e p e n d e t e 2 0 ⏞ i n d e p e n d e t e 1 0 0 1 1 0 0 0 0 0 0 0 0

Após o escalonamento, vemos que v 1 e v 3 são linearmente independentes. Portanto,

v 2 = a v 1 + b v 3 .

      2 - 4       0       6 = a       1 - 2       0       3 + b - 1       1       2       0   →     a = 2       b = 0 . Logo, v 3 = 2 v 1 .

Agora, v 4 = c v 1 + d v 3 .

      0 - 1       2       3 = c       1 - 2       0       3 + d - 1       1       2       0   →     c = 1       d = 1 . Logo, v 4 = v 1 + v 3 .

Passo 4

(c) Por fim, temos:

A =       1 - 2       4       0 - 7 - 1       3 - 5       4   18       5       1       9       2       2       2       0       4 - 3 - 8     →     Ã = 1 ⏞ i n d e p e n . 0 ⏞ i n d e p e n .       2 0 ⏞ i n d e p e n . - 1 0 1 - 1 0       3 0 0       0 1       2 0 0       0 0       0

Após o escalonamento, vemos que v 1 , v 2 e v 4 são linearmente independentes. Portanto,

v 3 = a v 1 + b v 2 + c v 4 .

      4 - 5       9       4 = a       1 - 1       5       2 + b - 2       3       1       0 + c       0       4       2 - 3   →     a = 2       b = - 1       c = 0 . Logo, v 3 = 2 v 1 - v 2 .

Agora, v 5 = d v 1 + e v 2 + f v 4 .

- 7   18       2 - 8 = d       1 - 1       5       2 + e - 2       3       1       0 + f       0       4       2 - 3   →     d = - 1       e = 3       f = 2 . Logo, v 5 = - v 1 + 3 v 2 + 2 v 4 .

Resposta

Veja a resolução completa.

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Suponha que A e B sejam matrizes n × n e que A seja invertível. Invente e prove um teorema que descreve como estão relacionados os espaços linha de A B e de B .
Encontre uma matriz 3 × 3 cujo espaço nulo seja(a) um ponto. (b) uma reta. (c) um plano.
Suponha que x 1 = - 1 , x 2 = 2 , x 3 = 4 , x 4 = - 3 seja uma solução de um sistema linear não homogêneo A x = b e que o conjunto solução do sistema homogêneo A x = 0 seja dado pela fórmulas x 1 = -
Em cada parte, encontre uma base do espaço nulo de A .(a) A = 1 - 13 5 - 4 - 4 7 - 62 (b) A = 2 0 - 1 4 0 - 2 0 00 (c) A =1 4 5 22 1 3 0 - 1 3 2 2 (d) A =145693 - 214 - 1 - 10 - 1 - 2 - 123578 (e) A =
Mostre que R θ 1 R θ 2 = R θ 1 + θ 2