Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.7 - Ex. 2c
Em cada parte, expresse o produto como uma combinação linear dos vetores coluna de A
Passo 1
Para expressar a combinação linear entre uma matriz e um vetor, basta associar as colunas da matriz, com as linhas do vetor:
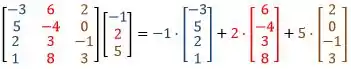
Então, a combinação linear entre a matriz e o vetor é:
Resposta
Exercícios de Livros Relacionados
Construa uma matriz cujo espaço nulo consista em todas as combinações lineares dos vetores v 1 =1 - 132 e v 2 =20 - 24
Em cada parte, encontre uma base do subespaço de R 4 gerado pelos vetores dados.(a) ( 1 ,1 ,- 4 ,- 3 ) ,( 2 ,0 ,2 ,- 2 ) ,( 2 ,- 1 ,3 ,2 ) (b) ( - 1 ,1 ,- 2 ,0 ) ,( 3 ,3 ,6 ,0 ) ,( 9 ,0 ,0 ,3 ) (c) (
Prove que os vetores linha de uma matriz invertível A de tamanho n × n formam uma base de R n .
Em cada parte, expresse o produto A x → como uma combinação linear dos vetores coluna de A 2 3 - 1 4 1 2