Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.7 - Ex. 3d
Em cada parte, determine se está no espaço coluna de e, se estiver, expresse como combinação linear dos vetores de
Passo 1
Um vetor está no espaço coluna de se a expressão abaixo for possível:
Então o que vamos fazer é conferir se existe algum vetor possível, e qual os valores desse vetor. Então vamos resolver o sistema abaixo:
Podemos solucionar utilizando Eliminação de Gauss Jordan.
Vamos pegar a segunda linha e somar na terceira linha:
Vamos pegar a primeira linha e somar na segunda linha:
Vamos dividir a segunda linha por
E por fim vamos pegar a segunda linha e subtrair na primeira:
Daqui chegamos em:
Passo 2
Agora podemos expressar a combinação linear:
Para expressar a combinação linear entre uma matriz e um vetor, basta associar as colunas da matriz, com as linhas do vetor:
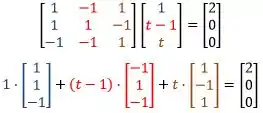
Então, a combinação linear entre a matriz e o vetor é: