Enunciado
Álgebra Linear e Geometria Analítica - Anton - Álgebra Linear- Ed: 10º - Capítulo 4.10 - Ex. 20
Em cada parte, use o Teorema 4.10.3 para encontrar a matriz canônica do operador matricial a partir das imagens dos vetores da base canônica
- As reflexões em da Tabela da Seção .
- As reflexões em da Tabela 2 da Seção 4.9.
- As projeções em da Tabela 3 da Seção 4.9.
- As projeções em da Tabela 4 da Seção 4.9.
- As rotações em da Tabela 5 da Seção 4.9.
- As dilatações e contrações em da Tabela 8 da Seção 4.9.
Passo 1
Vamos lá! o teorema 10.3 nos diz que:
TEOREMA 4.10.3 Toda transformação linear de em é uma transformação matricial
e, reciprocamente, toda transformação matricial de em é uma transformação
linear.
Agora vamos aplicar o teorema:
-
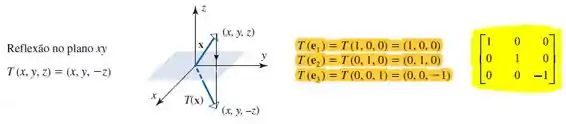
Para as reflexões em temos:
As matrizes marcadas em amarelo representam nossa matriz canônica a partir das imagens e
Passo 2
-
Para as reflexões em temos:
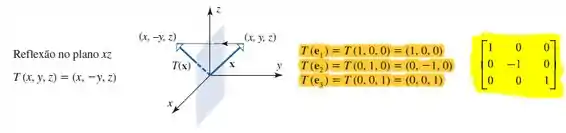
As matrizes marcadas em amarelo representam nossa matriz canônica a partir das imagens , e marcadas em laranja.
Passo 3
-
Para as projeções em temos:
As matrizes marcadas em amarelo representam nossa matriz canônica a partir das imagens e marcadas em laranja.
Passo 4
-
Para as projeções em temos:
As matrizes marcadas em amarelo representam nossa matriz canônica a partir das imagens , e marcadas em laranja.
Passo 5
-
Para as rotações em temos:
A matriz marcada em amarelo representa nossa matriz canônica a partir das equações lineares e marcadas em laranja.
Passo 6
Para as dilatações e contrações em temos:
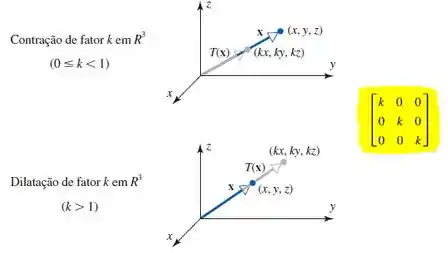
Sendo nossa imagem , temos a matriz canônica marcada em amarelo logo acima.
Resposta
Ei, a resposta está no passo a passo :)