Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.

30)

Sabendo que as equações genéricas da parábola são do tipo para quando o eixo da parábola é paralelo ao eixo , ou então para quando o eixo da parábola é paralelo ao , iremos reescrever a equação do exercício e comparar com as duas possibilidades:

Podemos observar que a equação reescrita no passo anterior é similar à equação da parábola com eixo paralelo ao eixo . Por comparação com a equação genérica , obtemos:

Agora, o vértice é dado pelas coordenadas . Assim, temos:

Como a equação é paralela ao eixo , devemos ter a coordenada de do foco igual à coordenada do vértice. Por outro lado, a coordenada é encontrada somando a coordenada do vértice, ou seja:

Portando, o foco é: .

A diretriz é encontrada subtraindo da coordenada do foco. A parábola possui eixo paralelo ao eixo , logo, a diretriz deve ser do tipo . Este valor será:

Por fim, devemos encontrar a equação para o eixo da parábola dada. Como esta equação é paralelo ao eixo (eu sei que já falei isso várias vezes), a equação deste eixo passa pela coordenada do foco, logo, esta equação deverá ser:

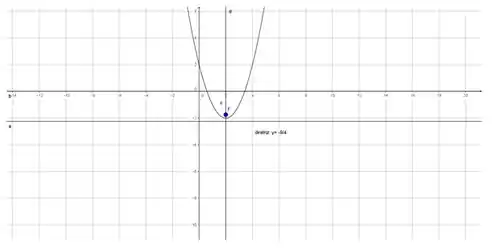
Com o auxílio do software Geogebra, plotamos o gráfico da função .