Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 22.Exercício - Ex. 112

Um espelho parabólico é obtido por rotação de uma parábola P em torno do seu eixo. Um raio luminoso parte do foco, atinge a superfície do espelho, e vai iluminar um ponto A de um anteparo. Determine a medida do ângulo agudo que o raio luminoso forma com o eixo da parábola, sabendo que o quociente entre a distância de A ao eixo e o parâmetro de P é 2 3 + 4 .

Passo 1

Veja o esquema a seguir.

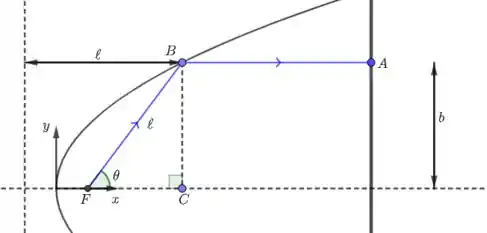
O raio de luz que sai de F atinge a parábola em um B . Pela propriedade da reflexão, sabemos que o raio de luz sairá paralelamente ao eixo da parábola. A única coisa que sabemos sobre a parábola é que

b p = 2 3 + 4

Passo 2

A equação da parábola poderá ser escrita como

y 2 = 4 p x

Assim, como B = p + b cot ⁡ θ ,   b :

b 2 = 4 p p + b cot ⁡ θ ∴ b 2 - 4 p 2 = 4 p b cot ⁡ θ ⟹ cot ⁡ θ = b 2 - 4 p 2 4 p b

Passo 3

Logo,

cot ⁡ θ = b 4 p - p b = 2 3 + 4 4 - 1 2 3 + 4 = 2 3 + 4 4 - 4 - 2 3 4 = 3

∴ cot ⁡ θ = 3 ⟹ θ = 30 °

Resposta

θ = 30 ° .

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.31)x 2 = 12 ( y - 6 )
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:13. foco: F 6,4 ; diretriz: y = - 2
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:7. vértice: V - 2,3 ; foco: F - 2,1
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:14. foco: F 3 , - 1 ; diretriz: x = 1 2
Em cada um dos problemas 1 a 18, estabelecer a equação de cada uma das parábolas, sabendo que:10. vértice: V 0,0 ; eixo y = 0 ; passa por 4,5 .