Sejam um ponto qualquer de uma parábola, distinto do vértice, sua projeção ortogonal sobre o eixo da parábola, e , respectivamente, os pontos que esse eixo intercepta a reta tangente e a reta normal em . Prove que o comprimento de não depende de , que o foco é ponto médio de , e que o vértice é o ponto médio de .

Vamos imaginar uma parábola do tipo , onde , sendo o parâmetro da parábola. Tomemos um ponto qualquer, determinamos e traçamos a reta tangente à parábola no ponto . Veja a figura abaixo:

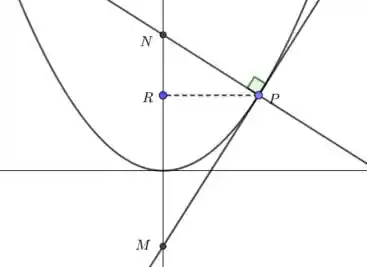
Seja , de modo que . A seguir, precisamos encontrar as coordenadas de e . Vamos determinar a equação da reta tangente à parábola em . Podemos fazer isso utilizando conceitos de derivada:

Lembrando que a derivada representa o coeficiente angular da reta tangente, segue que o coeficiente angular da reta tangente em é

Logo, a equação da reta tangente é:

Para encontramos as coordenadas de , basta fazer . Assim,

.

A seguir, vamos encontrar a equação da reta normal à parábola no ponto . Como a reta tangente e a reta normal são perpendiculares, segue que o coeficiente angular dessa reta, , é tal que:

Logo, a equação da reta normal é:

Para encontramos as coordenadas de , basta fazer . Logo,