Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.1.Problemas Propostos - Ex. 28
Em cada um dos problemas 19 a 34, determinar o vértice, o foco, uma equação para a diretriz e uma equação para o eixo da parábola de equação dada. Esboçar o gráfico.
27.
Passo 1
Vamos começar pela equação da nossa parábola mais geral, com vértice :
Mas antes precisamos deixar a equação da questão com a cara mais bonita e parecida com essa que temos genétrica da parábola, ne...
Vamos fazer o que chamamos de completar quadrados. É mais ou menos assim:
O você quer tranformar em algo como:
Bem.. lembra que:
Concorda que podemos escrever a equação da forma:
Então:
Comparando tudo, agora:
Então:
E:
Passo 2
Lembra que o sinal do só indica se a parábola é pra esquerda ou pra direita??? No nosso caso, como é negativo, então tem concavidade pra esquerda.
E que é a distância entre o foco e a diretriz (e também que o vértice está bem no meio de )
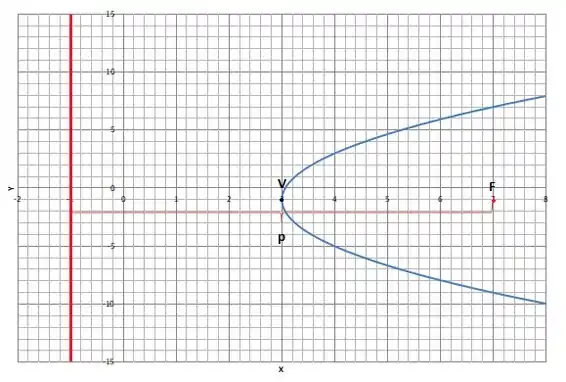
Então:
Foco:
Diretriz:
Eixo de simetria: