Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 5.Problemas Propostos - Ex. 52

Determinar os pontos de interseção da reta

r : y = 2 x - 3 z = - x + 2

Com os planos coordenados.

Passo 1

Queremos descobrir a interseção da reta entre planos coordenados, isso vai acontecer em 3 momentos. Teremos a interseção de x com y , onde z = 0 e vai ser o “chão” do nosso plano e nós chamaremos de x O y e será a zona azul do nosso plano.

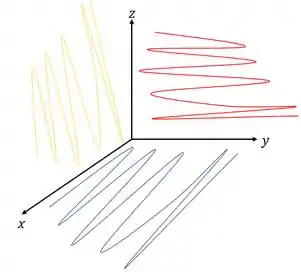
A outra interseção será do ponto x 0 z , onde y é nulo, representado pela zona amarela do plano cartesiano e a zona vermelha é z 0 y que acontece quando x é nulo, conforme a figura a seguir:

Passo 2

Vamos começar com a primeira interseção, em x O y com z = 0 . A equação que possui z é dada por:

z = - x + 2

Se z = 0 :

0 = - x + 2

Então:

x = 2

Substituindo na equação de y , teremos:

y = 2 x - 3

y = 2.2 - 3

y = 1

Então, nossa primeira coordenada é dada por ( 2,1 , 0 ) .

Passo 3

Agora, a segunda interseção, em x O z com   y = 0 . A equação que possui y é dada por:

y = 2 x - 3

Se y = 0 :

0 = 2 x - 3

Então:

3 = 2 x

x = 3 2

Substituindo na equação de z , teremos:

z = - x + 2

z = - 3 2 + 2 = - 3 + 4 2 = 1 2

Então, nossa primeira coordenada é dada por 3 2 , 0 , 1 2   .

Passo 4

A terceira interseção é dada por z 0 y , onde x = 0 . Substituindo nas equações temos:

y = 2 x - 3

y = 2.0 - 3

y = - 3

Substituindo em z :

z = - x + 2

z = 0 + 2

z = 2

Então, nossa coordenada será ( 0 , - 3,2 ) .

Resposta

2,1 , 0 ,   3 2 , 0 , 1 2   , ( 0 , - 3,2 )  

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Estabelecer equação reduzidas na variável x da reta de interseção dos planos: π 1 : x + y - z + 2 = 0 e π 2 : x + y + 2 z - 1 = 0
Determinar o ponto de interseção da reta r com o plano π . r : x = 4 + k y = 3 + 2 k z = - 2 - 3 k e π : x = 2 + h + 2 t y = - 3 - h - t z = 1 + 3 h - 3 t
Nos Problemas 19 a22 , os pares de retas r 1 e r 2 são paralelas ou concorrentes. Encontrar uma equação geral do plano que as contém.20) r 1 :x = 1 + 2 t y = - 2 + 3 t z = 3 - t r 2 :x = 1 - 2 t y = -
Nos Problemas 19 a22 , os pares de retas r 1 e r 2 são paralelas ou concorrentes. Encontrar uma equação geral do plano que as contém.19) r 1 :y = 2 x - 3 z = - x + 2 r 2 :x - 1 3 = z - 1 - 1 y = - 1
Nos Problemas 19 a22 , os pares de retas r 1 e r 2 são paralelas ou concorrentes. Encontrar uma equação geral do plano que as contém.21) r 1 :x = - 2 + t y = - t z = - 3 r 2 :y = - x - 1 z = 3