Enunciado
Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 8.Elipse - Ex. 25
Em cada um dos Problemas de 20 a 27, obter uma equação da elipse que satisfaça as condições dadas.
Centro , um vértice e excentricidade
Passo 1
Beleza, ele diz pra gente que o centro é em e temos um vértice em , então já podemos tirar que
E ele vai acompanhar .
Beleza, ele nos diz também que a excentricidade é , então temos que
E para achar só precisamos fazer aquela relação mágica do triangulo formado, se você não lembra, é essa aqui:
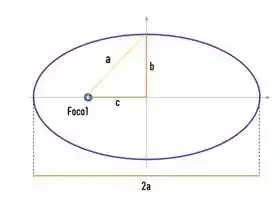
Então tiramos que
Passo 2
Agora vamos montar a nossa equação da elipse, lembrando que como o centro não está na origem, e o coeficiente acompanha , ficamos com essa equação:
Subsituindo os valores que temos de e e de e (são as coordenadas do centro) ficamos com:
Podemos ajeitar isso ai e ficamos com:
Resposta
Exercícios de Livros Relacionados
Percorrendo em sentido inverso as etapas na obtenção da equação 8 a partir da equação 1 , prove que se P x ,y for qualquer ponto cujas coordenadas satisfazem 8 , F P - + F ' P - = 2 a onde F e F ' são
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 4 . 16 x 2 + 9 y 2 = 1 44
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 5 . 2 x 2 + 3 y 2 = 18
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 2 . 4 x 2 + 9 y 2 = 4
Nos exercícios de 1 a 16, ache o centro, vértices, focos e extremidades do eixo menor da elipse dada. Faça um esboço da curva, mostrando os focos. 1 . 4 x 2 + 9 y 2 = 3 6