Enunciado
Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.2.Problemas Propostos - Ex. 17
Em cada um dos problemas 9 a 22, determinar a equação da elipse que satisfaz as condições dadas.
17) centro , um foco e tangente ao eixo dos .
Passo 1
Neste problema, precisamos determinar a equação da elipse que tem centro , um foco e tangente ao eixo dos .
Vamos lá? Aposto que vocês conseguem!
Passo 2
Inicialmente, vamos fazer uma figura que vai nos ajudar na determinação dos parâmetros desta elipse. Então, primeiro, vamos marcar os pontos conhecidos.
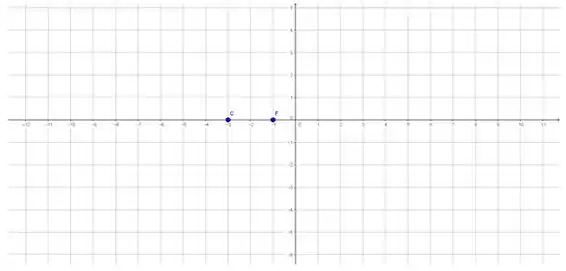
Passo 3
Em função do centro, podemos determinar o outro foco:
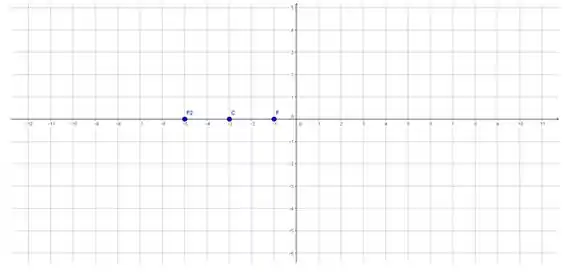
Portanto, a distância focal vale 4. Temos, então:
Passo 4
Então, como a elipse é tangente ao eixo dos , podemos marcar um dos vértices: .
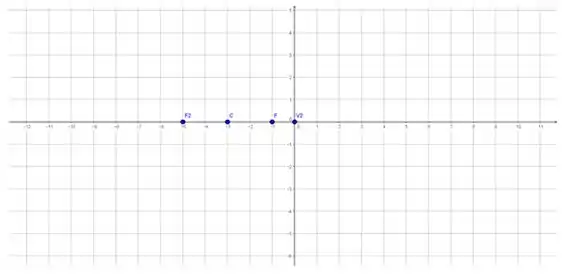
Passo 5
Agora, se liguem na maldade: em função da simetria em relação ao centro, podemos determinar o outro vértice:
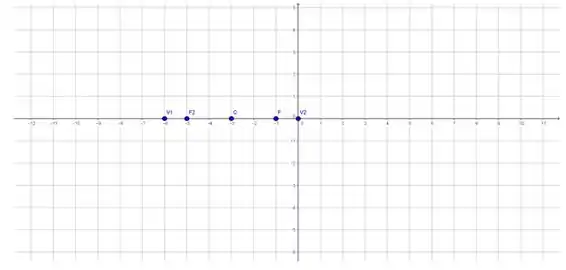
Passo 6
Feito isso, a distância entre os vértices vale 6. Temos, então:
Como , temos:
Passo 7
Por fim, a equação da elipse com eixo maior, paralelo ao eixo dos é dada por:
Portanto, a equação da elipse é: . 😉