Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Alfredo Steinbruch e Paulo Winterle - Geometria Analítica- Ed: 1º - Capítulo 7.2.Problemas Propostos - Ex. 6

Em cada um dos problemas 1 a 8, determinar os vértices A 1 e A 2 , os focos e as excentricidades das elipses dadas. Esboçar o gráfico.

6) 4 x 2 + y 2 = 1

Passo 1

Neste problema, precisamos determinar os vértices A 1 e A 2 , os focos e as excentricidades da elipse dada. Por último, ainda precisamos esboçar o gráfico. Vamos lá? Aposto que vocês conseguem!

Passo 2

Como o eixo maior está sobre o eixo dos y , sabemos que a equação da elipse vai ser dada por:

x 2 b 2 = y 2 a 2 = 1

A equação da elipse dada no enunciado tem a seguinte cara:

4 x 2 + y 2 = 1

Portanto, vamos reescrevê-la de um jeito mais bonitinho, para encontrarmos os valores de a e b :

4 x 2 + y 2 = 1

x 2 1 4 + y 2 1 = 1

Logo, por comparação, temos:

a 2 = 1 ⇒ a = 1

b 2 = 1 4 ⇒ b = 1 2  

Passo 3

Vamos agora achar a excentricidade da elipse, que é dada por:

e = c a

Como conhecemos os valores de a e b , podemos determinar c :

a 2 = b 2 + c 2

1 = 1 4 + c 2

c 2 = 3 4

c = 3 2

Portanto, a excentricidade é:

e = c a = 3 2 1 = 3 2

Passo 4

O centro da elipse é o ponto ( 0 ,   0 ) e os focos são dados por 0 ,   ± c = ( 0 ,   ± 3 2 ) .

Por último, os vértices são dados por 0 ,   ± a = 0 ,   ± 1 .

Passo 5

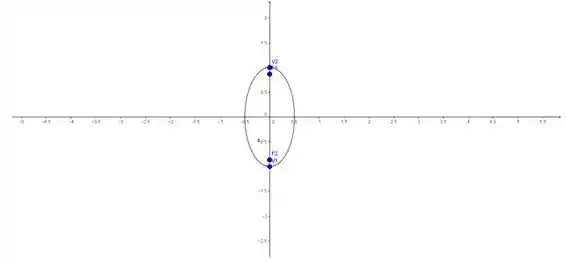
Logo, o gráfico é dado por:

Resposta

C 0 ,   0 ,     A 0 ,   ± 1 ,     F 0 ,   ± 3 2 ,     e = 3 2

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Ache a equação da elipse tendo as propriedades dadas e faça um esboço do gráfico.Centro na origem, focos sobre o eixo x , o comprimento do eixo maior é três vezes o do eixo menor e passa pelo ponto 3
43. Ao invés de seguir, no sentido inverso, as etapas usadas para obter a equação (8) a partir da equação (1), um método alternativo de obter (1) a partir de (8) é o seguinte: F P - + F ´ P - = x - c
Determine as retas tangentes á elipse E que são paralelas à reta s . aE : 4 x 2 + 2 y 2 = 1 , s : y = 2 x bE : x 2 p + y 2 q = 1 , s : y = m x
Quais são os pontos da elipse E : x 2 a 2 + y 2 b 2 = 1 em que a reta normal contém a o centro? b um foco?
Mostre que a regra prática para se obter uma equação da reta tangente no ponto T = h , k não exige que a equação da elipse esteja na forma reduzida: é suficiente que ela contenha apenas termos em x 2e