Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 1.O tratamento algébrico - Ex. 28c

28. Calcular a distância do ponto :

c) Ao plano .

Passo 1

Então pessoal, esse tipo de exercício só aparenta ser complicado, mas posso afirmar que não tem nada de monstruoso por aqui não, ok? Só precisamos entender o que o enunciado significa! Como o ponto que nos foi dado possui três coordenadas, então temos um gráfico tridimensional, onde o esboço desse ponto seria algo mais ou menos assim:

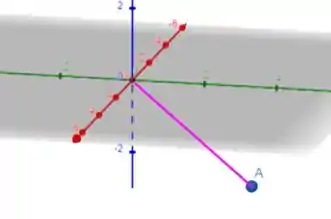
Aqui vale ressaltar que temos que olhar sob perspectiva! O eixo é a reta vermelha, o eixo é a reta verde e, por fim, o eixo é a reta azul. Show!

Passo 2

Agora que temos o gráfico, o que seria esse plano ? Esse plano seria uma superfície formada apenas pelas retas em verde e azul, galera. Em outras palavras, é como se quiséssemos calcular a distância do ponto ao plano com . Sendo assim, utilizando o teorema de Pitágoras, teremos:

E essa é a nossa distância!

Resposta

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

Sejam A, B e C vértices de um triângulo.Prove (algebricamente) que não existe o ponto X quando m +n = 0 . E interprete geometricamente este caso.

Os segmentos AN, BP e CM são dois a dois não paralelos. Dê uma condição necessária e suficiente sobre os vetores A N → , B P → e C M → , que não envolva suas normas, para que exista um triângulo de la

Sejam A , B e C pontos quaisquer, A ≠ B . Prove que: X pertence à reta A B se, e somente se, existem α e β tais que C X → = α C A → + β C B → e α + β = 1 ; X pertence ao segmento A B se, e somente se,

O ponto X divide A , B na razão α , Y divide B , C na razão β e Z divide C , A na razão γ . Exprima C X → , A Y → e B Z → em função de C A → , C B → , α , β , γ .

Dado o triângulo A B C , sejam X o ponto que divide A , B na razão 2 e Y o ponto que divide B , C na razão 3.Exprima C X → e A Y → em função de A B → , A C → .Prove que as retas CX e AY são concorrent