Enunciado
Álgebra Linear e Geometria Analítica - Paulo Boulos - Geometria Analítica - Ed: 3º - Capítulo 5.Exercício - Ex. 12
O ponto divide na razão , divide na razão e divide na razão . Exprima , e em função de , , , , .
Passo 1
Facilita bastante nos fazermos um simples esboço destes pontos e destas relações para questões deste tipo. Portanto, vamos ter uma ideia do que está ocorrendo:
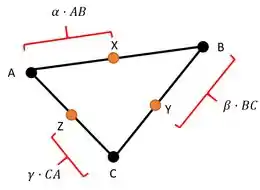
Esse simples esboço é o suficiente para nos ajudar a montar as nossas relações! Queremos expressar , e em função de , , , , . A dica, para isto, é ir somando vetores até obtemos o resultado que desejamos.
Passo 2
Bom, vamos começar pelo vetor . Portanto, temos:
Percebam que já conseguimos fazer aparecer um . O foco agora é transformar em uma soma de e . Para isto, sabemos que:
Mas também sabemos que:
E portanto,
Substituindo esta relação na equação de , temos:
E assim finalizamos o nosso primeiro vetor.
Passo 3
Vamos repetir todo o procedimento só que para o vetor . Portanto,
Percebam que já conseguimos fazer aparecer um . O foco agora é transformar em uma soma de e . Para isto, sabemos que:
Mas também sabemos que:
Portanto,
Substituindo esta relação na equação de , temos:
E assim finalizamos o nosso segundo vetor.
Passo 4
Para finalizarmos a questão, vamos calcular o vetor . Portanto,
Percebam que já conseguimos fazer aparecer um . O foco agora é transformar em uma soma de e . Para isto, sabemos que:
Portanto,
E assim terminamos a nossa questão.