Enunciado
Álgebra Linear e Geometria Analítica - LIMA, Elon L. Geometría analítica e Álgebra Linear- Ed: 2º - Capítulo 35.Problemas - Ex. 4
Calcule o determinante da matriz de Vandermonde:
Sem calcular o determinante, mostre diretamente que m, n e p são três números distintos então a matriz acima tem posto 3 (isto é, suas linhas são linearmente independentes)
Passo 1
Fala galerinha , vamos resolver mais uma questão do nosso livro de Geometria analítica e Álgebra Linear !!!
Primeiramente vamos lembrar que existe duas formas de determinar se uma matriz é linearmente independente - L.I ou não.
A primeira se o determinante for diferente de zero.
Sendo , vetores que compõem a matriz.
A segunda forma seria se os coeficientes multiplicados nos vetores serem iguais a zero, como mostra abaixo,
Onde,
Com isso em mente, vamos então ao próximo passo...
Passo 2
Este passo será provar a relação e encontrar o valor do determinante solicitado na questão.
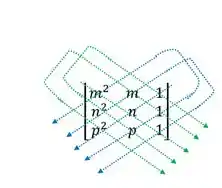
Passo 3
Agora vamos, mostrar que é L.I sem calcular o determinante. Para isto, vamos propor os seguinte vetores da matriz de Vandermonde
E usando a relação descrita no passo anterior,
Montando o sistema de equações, ficará,
No próximo passo, resolveremos o sistemas de equações para provar que,
Passo 4
Quase finalizando a questão galera !!!
Neste passo vamos encontrar os coeficientes
Substituindo na equação,
Substituindo na próxima equação,
Encontrando os próximos coeficientes,
E
E como também,
Resposta
Então, podemos concluir que a matriz de Vandermonde é L.I e com os coeficientes iguais a zero,
E de determinante igual,
Espero que ajudem nos estudos, até próxima