Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Vetores e uma iniciacao a geometria analitica mello e watanabe- Ed: 2º - Capítulo 2.Exercícios Propostos - Ex. 19

Calcule a para que os vetores   u →   = ( 2 a + 1 , a , 1 ) , v →   =   ( 2,0 , - 1 ) e w →   =   ( 0,1 , - 1 ) fiquem coplanares. A seguir expresse v →   como combinação linear de u → e w → .

Passo 1

Como já sabemos, os vetores coplanares são L.D. Então, a matriz formada por   u →   = ( 2 a + 1 , a , 1 ) , v →   =   ( 2,0 , - 1 ) e w →   =   ( 0,1 , - 1 ) tem, necessariamente, determinante nulo

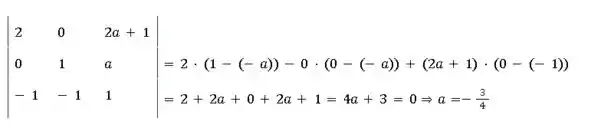
Com isso, concluímos que a = - 3 4 para que os três vetores sejam coplanares. Então, podemos escrever

u → = ( 2 a + 1 , a , 1 ) = ( - 3 2 + 1 , - 3 4 , 1 ) = ( - 1 2 , - 3 4 , 1 ) .

Passo 2

Agora, para expressar v →   como combinação linear de u → e w → , precisamos fazer

v →   = α u → + β w →

e igualar os dois lados para obter α e β . Então, temos

v →   = α u → + β w → ⇒   ( 2,0 , - 1 ) = α ( - 1 2 , - 3 4 , 1 ) + β ( 0,1 , - 1 ) = ( - α 2 , - 3 α 4 + β , α - β )

o que resulta no sistema de equações

- α 2 = 2 ⇒ α = - 4

- 3 α 4 + β = 0 ⇒ β = 3 α 4 = 3 4 ( - 4 ) = - 3

α - β = - 1

Substituindo os resultados que encontramos, vemos que

v →   = α u → + β w → = - 4 u → - 3 w →

Resposta

a = - 3 4

v →   = - 4 u → - 3 w →

Exercícios de Livros Relacionados

Mostrar que existe vetor cujos ângulos diretores são 30 ° , 90 ° e 60 ° , respectivamente, e determinar aquele que tem módulo 10 .
Para cada um dos pares de vetores u → e v → , encontrar a projeção ortogonal de v → sobre u → e decompor v → como soma de v → 1 com v → 2 , sendo v → 1 | | u → e v → 2 ⊥ u → . u → = 1,2 , - 2 e v → =
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Mostrar que A H - ⊥ B C - .
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Determinar o ponto H , pé da altura relativa ao vértice A .
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:Para qual valor de m o triângulo A B C é retângulo em A ?