Sejam , e vértices de um triângulo (Figura ) responda:
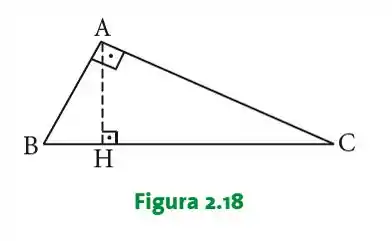
Determinar o ponto , pé da altura relativa ao vértice .
Passo 1
Vamos analisar a figura, podemos ver que a projeção de sobre a hipotenusa que calculamos na letra b) corresponde ao vetor , vamos usar essa informação para encontrar o ponto .
Temos que o vetor da projeção é:
Vamos então usar a expressão abaixo que possuem os pontos e junto com o vetor para assim encontrar o ponto :
Passo 2
Pronto, é só substituir então:
Viu, encontramos o ponto !