Responde Aí
Acesse com GoogleAcesse com AppleAcesse com Facebook

Enunciado

Álgebra Linear e Geometria Analítica - Paulo Winterle - Vetores e Geometria Analítica- Ed: 2º - Capítulo 2.Problemas Propostos - Ex. 43a

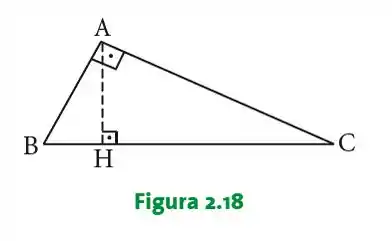
Sejam A 2,1 , 3 , B m , 3,5 e C 0,4 , 1 vértices de um triângulo (Figura 2.18 ) responda:

Para qual valor de m o triângulo A B C é retângulo em A ?

Passo 1

Se o triângulo A B C é retângulo em A temos que o ângulo entre os vetores A B → e A C → é de 90 ° , e de acordo com a fórmula abaixo o produto escalar entre os vetores A B → e A C → deve ser igual a zero, pois o cosseno de 90 ° é igual a zero:

A B → ⋅ A C → = A B → A C → cos ⁡ 90 ° = A B → A C → ⋅ 0 = 0

Vamos então resolver esse produto escalar para encontrar o valor de m .

Passo 2

Antes de calcular o produto escalar vamos primeiro achar os vetores A B → e A C → :

A B → = B - A = m , 3,5 - 2,1 , 3 = m - 2,3 - 1,5 - 3 = m - 2,2 , 2

A C → = C - A = 0,4 , 1 - 2,1 , 3 = 0 - 2,4 - 1,1 - 3 = - 2,3 , - 2

Agora sim vamos calcular o produto escalar:

A B → ⋅ A C → = 0 → m - 2,2 , 2 ⋅ - 2,3 , - 2 = 0 → m - 2 ⋅ - 2 + 2 ⋅ 3 + 2 ⋅ - 2 = 0 →

→ - 2 m + 4 + 6 - 4 = 0 → 2 m = 6 → m = 3

Pronto, temos que o valor de m é 3 para o triângulo A B C ser retângulo em A .

Resposta

m = 3

Ver Outros Exercícios desse livro

Exercícios de Livros Relacionados

12.Dados os pontos distintos A e B, seja X = A + α A B → . Em cada um dos casos, descreva o conjunto dos valores que α deve tomar para que X percorra todo o conjunto especificado. a ) O segmento A B b
São dadas as coordenadas de u → e v → em relação a uma base ortonormal fixada. Calcule, em radianos, a medida angular entre u → e v → . u → = 300 ,300 ,0 e v → = - 2000 , - 1000 ,2000
São dadas as coordenadas de u → e v → em relação a uma base ortonormal fixada. Calcule, em radianos, a medida angular entre u → e v → . u → = 3 ,3 ,0 e v → = ( 2 ,1 ,- 2 )
Verdadeiro ou falso?a) A medida angular entre um vetor não-nulo e ele mesmo é 0 (graus ou radianos).b) A medida angular entre dois vetores não-nulos e ortogonais é π / 2 radianos. c) A medida angular
Em uma roleta de centro O , o preto 17 ocupa a posição P . Após um giro de 7 π / 5 rad, passa a ocupar a posição Q . Qual é a medida angular em radianos entre O P → e O Q → ?